陕西省宝鸡市2022年初中学业水平模拟考试数学试卷（二）

更新时间：2024-07-13 浏览次数：85 类型：中考模拟

一、单选题

1. (2022·宝鸡模拟) （－3）＋2＝（）

A . －5 B . －1 C . 1 D . 5

答案解析收藏纠错 + 选题
2. (2022·宝鸡模拟) 若∠ $\text{[math]}$ ＝42°，则∠ $\text{[math]}$ 的补角的大小是（）

A . 138° B . 148° C . 48° D . 58°

答案解析收藏纠错 + 选题
3. (2022·宝鸡模拟) 下列计算正确的是（）

A . 3a＋4b＝12ab B . （ab²）³＝ab⁶ C . a²＋a²＝2a² D . （a＋3）²＝a²＋9

答案解析收藏纠错 + 选题
4. (2022·昭阳模拟) 直线a//b，其中∠1＝20°， ∠2＝36°，∠3为（）

A . 56° B . 124° C . 34° D . 36°

答案解析收藏纠错 + 选题
5. (2022·宝鸡模拟) 在正方形ABCD中，边AB＝1，E是CD中点，则线段OP长度为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 2 D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022·宝鸡模拟) 若函数y＝kx＋b由直线y＝－x＋2平移得到，且平移后的直线过点（2，1），则直线y＝kx＋b与y轴的交点坐标是（）

A . （0，－3） B . （3，0） C . （1，2） D . （0，3）

答案解析收藏纠错 + 选题
7. (2022·宝鸡模拟) 如图，△ABC中，∠ACB＝60°，AD⊥BC于D， BE⊥AC于E，AD与BE相交于点F，BD＝AD，AB ＝ $\text{[math]}$ ；则AF等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2022·宝鸡模拟) 已知二次函数y＝ax²－2ax＋a＋5（其中x是自变量）的图象上有两点（－2，y₁），（3，y₂），满足y₁＜y₂ ，当－2≦x＜3时，y的最小值为－4，则a的值为（）

A . －5 B . －1 C . 1 D . －2

答案解析收藏纠错 + 选题

二、填空题

9. (2023·临清模拟) 分解因式：4a﹣a³＝.

答案解析收藏纠错 + 选题
10. (2022·宝鸡模拟) 如图，在边长为1的正八边形ABCDEFGH中，连接AF，则AF＝.

答案解析收藏纠错 + 选题
11. (2022·宝鸡模拟) 如图是一组有规律的图案，图案1是由4个◆组成的，图案2是由7个◆组成的，图案3是由10个◆组成的，图案4是由13个◆组成的，依次类推，第n图案是由个◆组成的.

答案解析收藏纠错 + 选题
12. (2022·宝鸡模拟) 如图，在平面直角坐标系中，M是 $\text{[math]}$ ABCO的对称中心，点B的坐标为（6，4），若一个反比例函数的图象经过点M，交BC于点N，则N点的坐标是.

答案解析收藏纠错 + 选题
13. (2022·宝鸡模拟) 如图，四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ 且 $\text{[math]}$ ，则对角线BD长的最大值为.

答案解析收藏纠错 + 选题

三、解答题

14. (2022·宝鸡模拟) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
15. (2022·宝鸡模拟) 解方程组： $\text{[math]}$

答案解析收藏纠错 + 选题
16. (2022·宝鸡模拟) 化简： $\text{[math]}$

答案解析收藏纠错 + 选题
17. (2022·宝鸡模拟) 如图，△ABC中，AB＝AC，∠A＝36°，请你利用尺规在AC边上求一点P，使∠PBC＝36°.（不写画法，保留作图痕迹）

答案解析收藏纠错 + 选题
18. (2022·宝鸡模拟) 如图，在菱形ABCD中，E为AB上一点，延长BC至点F，使CF＝BE，连接CE、DF，求证CE＝DF.

答案解析收藏纠错 + 选题
19. (2022·宝鸡模拟) 习近平总书记来到陕西省柞水县小岭镇金米村实地考察，得知木耳喜获丰收.小木耳作出大产业，2019年王极东木耳一项净收入4万元，2021年净收入达到5.76万元，则两年的平均增长率是多少？

答案解析收藏纠错 + 选题
20. (2022·宝鸡模拟) “五一”期间，某超市为了吸引顾客，开展有奖促销活动，设立了一个可以自由转动的转盘，转盘被分为4个面积相等的扇形，四个扇形区域里分别标有“熊熊”、“朱朱”、“羚羚”、“金金”字样，它们分别表示以陕西秦岭独有的四个国宝级动物－大熊猫，朱鹮，羚牛、金丝猴为创意原型的毛绒玩具，超市规定：顾客在本超市每消费满100元，就可转动转盘一次，根据转盘指针指向区域获得相应的毛绒玩具.
1. （1）转动转盘一次，求得到“金金”的概率.
2. （2）小明家一次消费230元，转了两次转盘，用树状图或概率的方法，求小明希望得到一个“熊熊”和一个“金金”的概率.
答案解析收藏纠错 + 选题
21. (2022·宝鸡模拟) 宝鸡石鼓阁是中华石鼓园的两大标志性建筑之一，小明和小亮想知道石鼓阁的高度.在一个阳光明媚的下午，他们带着测量工具来到了石鼓阁前.在石鼓阁前平地上选择一点并且安装了测倾器CD，测得塔顶A的仰角为45°，小明又向前走了18米站到了F处，这时发现，他的影子刚好和石鼓阁影子的顶端重合.这时小亮测量得小明的影长为2米.已知测倾器CD高度为1米，小明身高为1.5米，他们俩利用所测量的数据很快算出了是石鼓阁的高度.请你根据他们俩的测量数据算出石鼓阁的高度是多少米？

答案解析收藏纠错 + 选题

22. (2022·宝鸡模拟) 为提高教育质量，落实立德树人的根本任务，中共中央办公厅、国务院办公厅印发了《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》，为切实减轻学生课后作业负担，某中学教务处随机抽取了七、八、九年级部分学生并对这些学生家庭作业所用时间进行了调查.现将调查结果分为A，B，C，D、E组.同时，将调查的结果绘成了两幅不完整的统计图.

组别	人数	时间（小时）
A	20	0≤t＜0.5
B	40	0.5≤t＜1
C	m	1≤t＜1.5
D	12	1.5≤t＜2
E	8	2≤t

请你根据以上信息，解答下列问题：

（1）表格中的m＝，扇形统计图中的n＝.
（2）所抽取的学生完成家庭作业的众数为组别.
（3）已知该校有学生2600人，请你估计该校有多少人的家庭作业时间在1.5小时以内？

答案解析收藏纠错 + 选题

23. (2022·宝鸡模拟) “相约西安，筑梦全运”，2021年9月15日至27日，第十四届全运会在陕西西安举行.小明一家开车去观看比赛，将油箱加满油后进行了油耗试验，得到如下数据：

轿车行使路程x（km）	0	10	20	30	40	…
油箱剩余油量y（1）	50	49.3	48.6	47.9	47.2	…

（1）根据上表数据，求邮箱剩余油量y（1）与轿车行使的路程x（km）之间的函数关系式；
（2）小明将油箱加满后，驾车从家到西安，到达西安时剩余油量为29L，求小明家到西安的距离？若小明一家返回途中，最多可行驶多少千米？（精确到个位）

答案解析收藏纠错 + 选题

24. (2022·宝鸡模拟) 如图，AC是⊙O的直径，B在⊙O上，BD平分∠ABC交⊙O于点D，过点D作DE∥AC交BC的延长线于点E.
1. （1）求证：DE是⊙O的切线.
2. （2）若AB＝4，BC＝2，求BE的长.
答案解析收藏纠错 + 选题
25. (2022·宝鸡模拟) 在平面直角坐标系中已知抛物线 $\text{[math]}$ 经过点 $\text{[math]}$ 和点 $\text{[math]}$ ，点D为抛物线的顶点.
1. （1）求抛物线 $\text{[math]}$ 的表达式及点D的坐标；
2. （2）将抛物线 $\text{[math]}$ 关于点 $\text{[math]}$ 对称后的抛物线记作 $\text{[math]}$ ，抛物线 $\text{[math]}$ 的顶点记作点E，求抛物线 $\text{[math]}$ 的表达式及点 $\text{[math]}$ 的坐标；
3. （3）是否在 $\text{[math]}$ 轴上存在一点 $\text{[math]}$ ，在抛物线 $\text{[math]}$ 上存在一点 $\text{[math]}$ ，使 $\text{[math]}$ 为顶点的四边形是平行四边形？若存在，请求出 $\text{[math]}$ 点坐标，若不存在，请说明理由.
答案解析收藏纠错 + 选题
26. (2022·宝鸡模拟) 用如图①，②所示的两个直角三角形（部分边长及角的度数在图中已标出），完成以下两个探究问题：

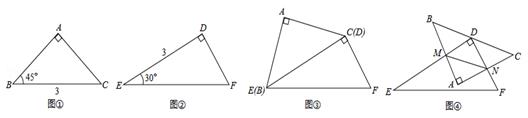
探究一：将以上两个三角形如图③拼接（BC和ED重合），在BC边上有一动点P.
1. （1）当点P运动到∠CFB的角平分线上时，连接AP，求线段AP的长；
2. （2）当点P在运动的过程中出现PA=FC时，求∠PAB的度数.
  探究二：如图④，将△DEF的顶点D放在△ABC的BC边上的中点处，并以点D为旋转中心旋转△DEF，使△DEF的两直角边与△ABC的两直角边分别交于M、N两点，连接MN.在旋转△DEF的过程中，△AMN的周长是否存在有最小值？若存在，求出它的最小值；若不存在，请说明理由.
答案解析收藏纠错 + 选题