 B .
B .  C .
C .  D .
D . 


 B .
B . 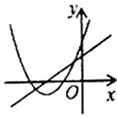 C .
C . 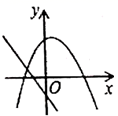 D .
D . 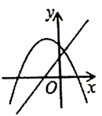









如图2,在四边形中,
与
互余,小明发现四边形
中这对互余的角可类比(1)中思路进行拼合:先作
, 再过点
作
于点
, 连接
, 发现
,
,
之间的数量关系是;

如图3,在四边形中,连接
,
, 点
是
两边垂直平分线的交点,连接
,
.
①求证:;
②连接 , 如图4,已知
,
,
, 求
的长(用含
,
的式子表示).
