 B .
B .  C .
C .  D .
D . 
 C .
C .  D .
D . 





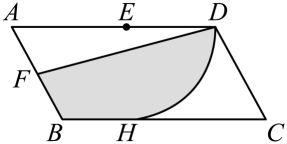


(参考数据:sin37° , cos37°
, tan37°
, 计算结果保留根号)



各边长都是整数,最大边长为31的三角形有多少个?
问题建模:为解决上面的数学问题,我们先研究下面的数学模型。
在1~n这n个自然数中,每次取两个数(可重复),使得所取的两个数之和大于n,有多少种不同的取法?
为了找到解决问题的方法,我们把上面数学模型简单化.
探究一:
在1~4这4个自然数中,每次取两个数(可重复),使得所取的两个数之和大于4,有多少种不同的取法?
第一步:在1~4这4个自然数中,每次取两个不同的数,使得所取的两个数之和大于4,根据题意,有下列取法:1+4,2+3,2+4,3+2,3+4,4+1,4+2,4+3;而1+4与4+1,2+3与3+2,…是同一种取法,所有上述每一种取法都重复过一次,因此共有种不同的取法.
第二步:在1~4这4个自然数中,每次取两个相同的数,使得所取的两个数之和大于4,有下列取法:3+3,4+4,因此有2种不同的取法.
综上所述,在1~4这4个自然数中,每次取两个数(可重复),使得所取的两个数之和大于4,有种不同的取法.
探究二:
在1~5这5个自然数中,每次取两个数(可重复),使得所取的两个数之和大于5,有多少种不同的取法?
第一步:在1~5这5个自然数中,每次取两个不同的数,使得所取的两个数之和大于5,根据题意,有下列取法:1+5,2+4,2+5,3+4,3+5,4+2,4+3,4+5,5+1,5+2,5+3,5+4;而1+5与5+1,2+4与4+2,…是同一种取法,所有上述每一种取法都重复过一次,因此共有种不同的取法.
第二步:在1~5这5个自然数中,每次取两个相同的数,使得所取的两个数之和大于5,有下列取法:3+3,4+4,5+5因此有3种不同的取法.
综上所述,在1~5这5个自然数中,每次取两个数(可重复),使得所取的两个数之和大于5,有种不同的取法.
探究三:
在1~6这6个自然数中,每次取两个数(可重复),使得所取的两个数之和大于6,有多少种不同的取法?(仿照探究二写出探究过程)
探究四:
在1~7这7个自然数中,每次取两个数(可重复),使得所取的两个数之和大于7,有 ▲ 种不同的取法.
探究五:
在1~n(n为偶数)这n个自然数中,每次取两个数(可重复),使得所取的两个数之和大于n,有 ▲ 种不同的取法.
探究六:
在1~n(n为奇数)这n个自然数中,每次取两个数(可重复),使得所取的两个数之和大于n,有 ▲ 种不同的取法.
问题解决:
①各边长都是整数,最大边长为20的三角形有 ▲ 个;
②各边长都是整数,最大边长为31的三角形有 ▲ 个.
解答下列问题:
