山东省潍坊市2022届高三下学期数学二模试卷

更新时间：2022-05-24 浏览次数：82 类型：高考模拟

一、单选题

1. (2022·潍坊二模) 设M，N，U均为非空集合，且满足 $\text{[math]}$ ⫋ $\text{[math]}$ ⫋ $\text{[math]}$ ，则 $\text{[math]}$ （）

A . M B . N C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022·潍坊二模) 已知直线 $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . 3 D . －3

答案解析收藏纠错 + 选题
3. (2022·潍坊二模) 已知角 $\text{[math]}$ 的顶点为坐标原点，始边与x轴的非负半轴重合，点 $\text{[math]}$ ， $\text{[math]}$ 在角 $\text{[math]}$ 的终边上，且 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . 2 B . $\text{[math]}$ C . -2 D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2022·潍坊二模) 十七世纪，数学家费马提出猜想：“对任意正整数 $\text{[math]}$ ，关于x，y，z的方程 $\text{[math]}$ 没有正整数解”，经历三百多年，1995年数学家安德鲁·怀尔斯给出了证明，使它终成费马大定理，则费马大定理的否定为（）

A . 对任意正整数n，关于x，y，z的方程 $\text{[math]}$ 都没有正整数解 B . 对任意正整数 $\text{[math]}$ ，关于x，y，z的方程 $\text{[math]}$ 至少存在一组正整数解 C . 存在正整数 $\text{[math]}$ ，关于x，y，z的方程 $\text{[math]}$ 至少存在一组正整数解 D . 存在正整数 $\text{[math]}$ ，关于x，y，z的方程 $\text{[math]}$ 至少存在一组正整数解

答案解析收藏纠错 + 选题
5. (2023高一上·嘉兴月考) 已知函数 $\text{[math]}$ （ $\text{[math]}$ 且 $\text{[math]}$ ）的图像如图所示，则以下说法正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022·潍坊二模) 某学校为增进学生体质，拟举办长跑比赛，该学校高一年级共有6个班，现将8个参赛名额分配给这6个班，每班至少1个参赛名额，则不同的分配方法共有（）

A . 15种 B . 21种 C . 30种 D . 35种

答案解析收藏纠错 + 选题
7. (2022·潍坊二模) 已知正实数a，b满足 $\text{[math]}$ ，则a+2b的最大值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 2

答案解析收藏纠错 + 选题
8. (2022·潍坊二模) 已知函数 $\text{[math]}$ ，直线 $\text{[math]}$ ，点 $\text{[math]}$ 在函数 $\text{[math]}$ 图像上，则以下说法正确的是（）

A . 若直线l是曲线 $\text{[math]}$ 的切线，则 $\text{[math]}$ B . 若直线l与曲线 $\text{[math]}$ 无公共点，则 $\text{[math]}$ C . 若 $\text{[math]}$ ，则点P到直线l的最短距离为 $\text{[math]}$ D . 若 $\text{[math]}$ ，当点P到直线l的距离最短时， $\text{[math]}$

答案解析收藏纠错 + 选题

二、多选题

9. (2022·潍坊二模) 若复数 $\text{[math]}$ ， $\text{[math]}$ ，其中 $\text{[math]}$ 是虚数单位，则下列说法正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 若 $\text{[math]}$ 是纯虚数，那么 $\text{[math]}$ D . 若 $\text{[math]}$ 在复平面内对应的向量分别为 $\text{[math]}$ （ $\text{[math]}$ 为坐标原点），则 $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2022·潍坊二模) 已知函数 $\text{[math]}$ 的图象为C，则（）

A . 图象C关于直线 $\text{[math]}$ 对称 B . 图象C关于点 $\text{[math]}$ 中心对称 C . 将 $\text{[math]}$ 的图象向左平移 $\text{[math]}$ 个单位长度可以得到图象C D . 若把图象C向左平移 $\text{[math]}$ 个单位长度，得到函数 $\text{[math]}$ 的图象，则函数 $\text{[math]}$ 是奇函数

答案解析收藏纠错 + 选题
11. (2022·潍坊二模) 已知四面体ABCD的4个顶点都在球O（O为球心）的球面上，△ABC为等边三角形，M为底面ABC内的动点，AB=BD=2， $\text{[math]}$ ，且 $\text{[math]}$ ，则（）

A . 平面ACD⊥平面ABC B . 球心O为△ABC的中心 C . 直线OM与CD所成的角最小为 $\text{[math]}$ D . 若动点M到点B的距离与到平面ACD的距离相等，则点M的轨迹为抛物线的一部分

答案解析收藏纠错 + 选题
12. (2022·潍坊二模) 已知数列 $\text{[math]}$ ， $\text{[math]}$ ，有 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则（）

A . 若存在 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ B . 若 $\text{[math]}$ ，则存在大于2的正整数n，使得 $\text{[math]}$ C . 若 $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ D . 若 $\text{[math]}$ ， $\text{[math]}$ ，则关于 $\text{[math]}$ 的方程 $\text{[math]}$ 的所有实数根可构成一个等差数列

答案解析收藏纠错 + 选题

三、填空题

13. (2022·潍坊二模) 设随机变量X服从标准正态分布 $\text{[math]}$ ，那么对于任意a，记 $\text{[math]}$ ，已知 $\text{[math]}$ ，则 $\text{[math]}$ =．

答案解析收藏纠错 + 选题
14. (2022·潍坊二模) 若圆 $\text{[math]}$ 与圆 $\text{[math]}$ 的交点为A，B，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
15. (2022·潍坊二模) 已知定义在 $\text{[math]}$ 上的函数 $\text{[math]}$ 满足 $\text{[math]}$ ，且当 $\text{[math]}$ 时， $\text{[math]}$ $\text{[math]}$ 图像与x轴的交点从左至右为O， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， …， $\text{[math]}$ ， …； $\text{[math]}$ 图像与直线 $\text{[math]}$ 的交点从左至右为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， …， $\text{[math]}$ ， …．若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， …， $\text{[math]}$ 为线段 $\text{[math]}$ 上的10个不同的点，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
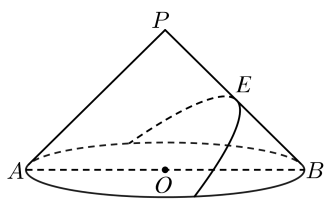
16. (2022·潍坊二模) 根据高中的解析几何知识，我们知道平面与圆锥面相交时，根据相交的角度不同，可以是三角形、圆、椭圆、抛物线、双曲线．如图，AB是圆锥底面圆O的直径，圆锥的母线 $\text{[math]}$ ， $\text{[math]}$ ， E是其母线PB的中点．若平面 $\text{[math]}$ 过点E，且PB⊥平面 $\text{[math]}$ ，则平面 $\text{[math]}$ 与圆锥侧面的交线是以E为顶点的抛物线的一部分，此时抛物线的焦点F到底面圆心O的距离为；截面 $\text{[math]}$ 把圆锥分割成两部分，在两部分内部，分别在截面 $\text{[math]}$ 的上方作一个半径最大的球M，在截面 $\text{[math]}$ 下方作一个半径最大的球N，则球M与球N的半径的比值为．

答案解析收藏纠错 + 选题

四、解答题

17. (2022·潍坊二模) 如图，四边形 $\text{[math]}$ 的内角 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ ．
1. （1）求 $\text{[math]}$ ；
2. （2）若点 $\text{[math]}$ 是线段 $\text{[math]}$ 上的一点， $\text{[math]}$ ，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
18. (2022·潍坊二模) 如图，线段AC是圆O的直径，点B是圆O上异于A，C的点， $\text{[math]}$ ， $\text{[math]}$ ， PA⊥底面ABC，M是PB上的动点，且 $\text{[math]}$ ， N是PC的中点．
1. （1）若 $\text{[math]}$ 时，记平面AMN与平面ABC的交线为l，试判断直线l与平面PBC的位置关系，并加以证明；
2. （2）若平面PBC与平面ABC所成的角为 $\text{[math]}$ ，点M到平面PAC的距离是 $\text{[math]}$ ，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
19. (2022·潍坊二模) 已知正项数列 $\text{[math]}$ 的前n项和为 $\text{[math]}$ ，且 $\text{[math]}$ ，数列 $\text{[math]}$ 满足 $\text{[math]}$ ．
1. （1）求数列 $\text{[math]}$ 的前n项和 $\text{[math]}$ ，并证明 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是等差数列；
2. （2）设 $\text{[math]}$ ，求数列 $\text{[math]}$ 的前n项和 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
20. (2022·潍坊二模) 已知函数 $\text{[math]}$ ．
1. （1）若 $\text{[math]}$ ，当 $\text{[math]}$ 时，求证： $\text{[math]}$ 为单调递减函数；
2. （2）若 $\text{[math]}$ 在 $\text{[math]}$ 上恒成立，求实数a的取值范围．
答案解析收藏纠错 + 选题
21. (2022·潍坊二模) 随着互联网的快速发展和应用，越来越多的人开始选择网上购买产品和服务．某网购平台为提高2022年的销售额，组织网店开展“秒杀”抢购活动，甲，乙，丙三人计划在该购物平台分别参加 $\text{[math]}$ 三家网店各一个订单的“秒杀”抢购，已知三人在 $\text{[math]}$ 三家网店订单“秒杀”成功的概率均为 $\text{[math]}$ ，三人是否抢购成功互不影响．记三人抢购到的订单总数为随机变量 $\text{[math]}$ ．
1. （1）求 $\text{[math]}$ 的分布列及 $\text{[math]}$ ；
2. （2）已知每个订单由 $\text{[math]}$ 件商品构成，记三人抢购到的商品总数量为 $\text{[math]}$ ，假设 $\text{[math]}$ ，求 $\text{[math]}$ 取最小值时正整数 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
22. (2022·潍坊二模) 已知M，N为椭圆 $\text{[math]}$ 和双曲线 $\text{[math]}$ 的公共顶点， $\text{[math]}$ ， $\text{[math]}$ 分别为 $\text{[math]}$ 和 $\text{[math]}$ 的离心率．
1. （1）若 $\text{[math]}$ ．
  （ⅰ）求 $\text{[math]}$ 的渐近线方程；
  （ⅱ）过点 $\text{[math]}$ 的直线l交 $\text{[math]}$ 的右支于A，B两点，直线MA，MB与直线 $\text{[math]}$ 相交于 $\text{[math]}$ ， $\text{[math]}$ 两点，记A，B， $\text{[math]}$ ， $\text{[math]}$ 的坐标分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求证： $\text{[math]}$ ；
2. （2）从 $\text{[math]}$ 上的动点 $\text{[math]}$ 引 $\text{[math]}$ 的两条切线，经过两个切点的直线与 $\text{[math]}$ 的两条渐近线围成三角形的面积为S，试判断S是否为定值？若是，请求出该定值；若不是，请说明理由．
答案解析收藏纠错 + 选题