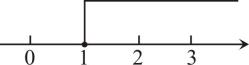
 B .
B . 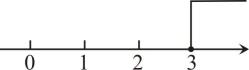 C .
C . 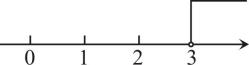 D .
D . 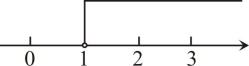

【分析问题】先根据已知条件用一个量如取y表示另一个量如x,然后根据题中已知量x的取值范围,构建另一个量y的不等式,从而确定该量y的取值范围,同法再确定另一未知量x的取值范围,最后利用不等式性质即可获解.
【解决问题】解:∵x﹣y=2,∴x=y+2.
又∵x>1,∴y+2>1,∴y>﹣1.
又∵y<0,∴﹣1<y<0,…①
同理得1<x<2…②
由①+②得﹣1+1<y+x<0+2.
∴x+y的取值范围是0<x+y<2.
【尝试应用】已知x﹣y=﹣3,且x<﹣1,y>1,求x+y的取值范围.
A种产品 | B种产品 | |
成本(万元/件) | 2 | 5 |
利润(万元/件) | 1 | 3 |