河南省郑州市2022届高三理数第三次质量预测试卷

更新时间：2022-06-08 浏览次数：70 类型：高考模拟

一、单选题

1. (2022·郑州模拟) 设全集 $\text{[math]}$ ，集合 $\text{[math]}$ ， $\text{[math]}$ ，则下面Venn图中阴影部分表示的集合是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022·郑州模拟) 在复平面内，复数 $\text{[math]}$ （其中i为虚数单位）对应的点位于（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
3. (2022·郑州模拟) 已知等比数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和为 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 1 D . -1

答案解析收藏纠错 + 选题
4. (2022·郑州模拟) 设函数 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . 5 B . 6 C . 7 D . 8

答案解析收藏纠错 + 选题
5. (2022·郑州模拟) 已知 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022·郑州模拟) 用一个平面截正方体，截面可能出现的形状是（）
①等边三角形②直角梯形③菱形④五边形

A . ①②③ B . ①②④ C . ①③④ D . ②③④

答案解析收藏纠错 + 选题
7. (2022·郑州模拟) 在 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 上一点， $\text{[math]}$ ， $\text{[math]}$ 是线段 $\text{[math]}$ 上一点， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
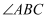
8. (2023·内江模拟) 位于登封市告成镇的观星台相当于一个测量日影的圭表．圭表是我国古代一种通过测量正午日影长度来推定节气的天文仪器，它包括一根直立的标竿（称为“表”）和一把呈南北方向水平固定摆放的与标竿垂直的长尺（称为“圭”）．当正午太阳照射在表上时，日影便会投影在圭面上，圭面上日影长度最长的那一天定为冬至，日影长度最短的那一天定为夏至．如图是一个根据郑州市的地理位置设计的圭表的示意图，已知郑州市冬至正午太阳高度角（即 $\text{[math]}$ ）约为32.5°，夏至正午太阳高度角（即 $\text{[math]}$ ）约为79.5°，圭面上冬至线与夏至线之间的距离（即 $\text{[math]}$ 的长）为14米，则表高（即 $\text{[math]}$ 的长）约为（）（其中 $\text{[math]}$ ， $\text{[math]}$ ）

A . 9.27米 B . 9.33米 C . 9.45米 D . 9.51米

答案解析收藏纠错 + 选题
9. (2022·郑州模拟) 已知函数 $\text{[math]}$ 的一条对称轴方程为 $\text{[math]}$ ，把函数 $\text{[math]}$ 的图象上所有的点向左平移 $\text{[math]}$ 个单位，可得到函数 $\text{[math]}$ 的图象，若函数 $\text{[math]}$ 为奇函数，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2022·郑州模拟) 已知抛物线 $\text{[math]}$ 的焦点为 $\text{[math]}$ ，过 $\text{[math]}$ 的直线交抛物线于 $\text{[math]}$ ， $\text{[math]}$ 两点，则 $\text{[math]}$ 的最小值为（）

A . 6 B . 9 C . 12 D . 15

答案解析收藏纠错 + 选题
11. (2022·郑州模拟) 如图，已知正方体 $\text{[math]}$ 的棱长为2，点 $\text{[math]}$ 是棱 $\text{[math]}$ 的中点， $\text{[math]}$ 是侧面 $\text{[math]}$ 内的动点，且 $\text{[math]}$ 平面 $\text{[math]}$ ，当 $\text{[math]}$ 的外接圆面积最小时，则三棱锥 $\text{[math]}$ 的外接球的表面积为（）

A . 8π B . 9π C . 10π D . 12π

答案解析收藏纠错 + 选题
12. (2022·郑州模拟) 已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则它们的大小关系正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

13. (2022·郑州模拟) 设变量 $\text{[math]}$ ， $\text{[math]}$ 满足约束条件 $\text{[math]}$ 则 $\text{[math]}$ 的最大值为．

答案解析收藏纠错 + 选题
14. (2022·郑州模拟) 函数 $\text{[math]}$ 的图象在 $\text{[math]}$ 处切线的倾斜角为．

答案解析收藏纠错 + 选题
15. (2022·郑州模拟) 党的十九大报告提出“乡村振兴战略”，要“推动城乡义务教育一体化发展，高度重视农村义务教育”．为了响应报告精神，某师范大学6名毕业生主动申请到某贫困山区的乡村小学工作，若将这6名毕业生分配到该山区的3所乡村小学，每所学校至少分配1人，则分配方案的总数为．

答案解析收藏纠错 + 选题
16. (2022·郑州模拟) 在△ $\text{[math]}$ 中，角 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 所对的边分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．若 $\text{[math]}$ ， $\text{[math]}$ ，则△ $\text{[math]}$ 面积的最小值是．

答案解析收藏纠错 + 选题

三、解答题

17. (2022·郑州模拟) 已知数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和为 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）证明数列 $\text{[math]}$ 为等差数列；
2. （2）求数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
18. (2022·郑州模拟) 如图，四棱锥 $\text{[math]}$ 中， $\text{[math]}$ 平面 $\text{[math]}$ ，底面 $\text{[math]}$ 为菱形， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 上一点， $\text{[math]}$ ．
1. （1）若 $\text{[math]}$ 平面 $\text{[math]}$ ，求实数 $\text{[math]}$ 的值；
2. （2）在（1）的条件下，若 $\text{[math]}$ ，求二面角 $\text{[math]}$ 的正弦值．
答案解析收藏纠错 + 选题
19. (2022高三上·沈阳月考) 据悉强基计划的校考由试点高校自主命题，校考过程中达到笔试优秀才能进入面试环节．已知甲、乙两所大学的笔试环节都设有三门考试科目且每门科目是否达到优秀相互独立．若某考生报考甲大学，每门科目达到优秀的概率均为 $\text{[math]}$ ，若该考生报考乙大学，每门科目达到优秀的概率依次为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，其中 $\text{[math]}$ ．
1. （1）若 $\text{[math]}$ ，分别求出该考生报考甲、乙两所大学在笔试环节恰好有一门科目达到优秀的概率；
2. （2）强基计划规定每名考生只能报考一所试点高校，若以笔试过程中达到优秀科目个数的期望为依据作出决策，该考生更希望进入甲大学的面试环节，求 $\text{[math]}$ 的范围．
答案解析收藏纠错 + 选题
20. (2022·郑州模拟) 设 $\text{[math]}$ 、 $\text{[math]}$ 分别为椭圆 $\text{[math]}$ 的左、右顶点，设 $\text{[math]}$ 是椭圆下顶点，直线 $\text{[math]}$ 与 $\text{[math]}$ 斜率之积为 $\text{[math]}$ ．
1. （1）求椭圆 $\text{[math]}$ 的标准方程；
2. （2）若一动圆的圆心 $\text{[math]}$ 在椭圆上运动，半径为 $\text{[math]}$ ．过原点 $\text{[math]}$ 作动圆 $\text{[math]}$ 的两条切线，分别交椭圆于 $\text{[math]}$ 、 $\text{[math]}$ 两点，试证明 $\text{[math]}$ 为定值．
答案解析收藏纠错 + 选题
21. (2022·郑州模拟) 设函数 $\text{[math]}$ ．
1. （1）求函数 $\text{[math]}$ 的单调区间；
2. （2）若 $\text{[math]}$ 存在两个极值点 $\text{[math]}$ ， $\text{[math]}$ ，证明： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
22. (2022·郑州模拟) 在直角坐标系 $\text{[math]}$ 中，曲线 $\text{[math]}$ 的方程为 $\text{[math]}$ ． $\text{[math]}$ 为曲线 $\text{[math]}$ 上一动点，且 $\text{[math]}$ ，点 $\text{[math]}$ 的轨迹为曲线 $\text{[math]}$ ．以坐标原点为极点， $\text{[math]}$ 轴正半轴为极轴建立极坐标系．
1. （1）求曲线 $\text{[math]}$ ， $\text{[math]}$ 的极坐标方程；
2. （2）曲线 $\text{[math]}$ 的极坐标方程为 $\text{[math]}$ ，点 $\text{[math]}$ 为曲线 $\text{[math]}$ 上一动点，求 $\text{[math]}$ 的最大值．
答案解析收藏纠错 + 选题
23. (2022·郑州模拟) 已知函数 $\text{[math]}$ ．
1. （1）若 $\text{[math]}$ ，求不等式 $\text{[math]}$ 的解集；
2. （2）若 $\text{[math]}$ 时，函数 $\text{[math]}$ 的图像与直线 $\text{[math]}$ 所围成图形的面积为 $\text{[math]}$ ，求实数 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题