重庆市2022年中考数学试卷（B卷）

更新时间：2022-06-17 浏览次数：434 类型：中考真卷

一、选择题（共12个小题，每小题4分，共48分）

1. (2022·重庆) −2 的相反数是（）

A . -2 B . 2 C . - $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022七下·清苑期末) 下列北京冬奥会运动标识图案是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2022·重庆) 如图，直线 a∥b，直线 m 与 a，b 相交，若∠1=115°，则∠2 的度数为（）

A . 115° B . 105° C . 75° D . 65°

答案解析收藏纠错 + 选题
4. (2023七下·永安期中) 如图是小颖 0 到 12 时的心跳速度变化图，在这一时段内心跳速度最快的时刻约为（）

A . 3时 B . 6时 C . 9时 D . 12时

答案解析收藏纠错 + 选题
5. (2022·重庆) 如图，△ABC 与△DEF 位似，点 O 是它们的位似中心，且相似比为 1：2，则△ABC 与△DEF 的周长之比是（）

A . 1：2 B . 1：4 C . 1：3 D . 1：9

答案解析收藏纠错 + 选题
6. (2023·重庆市模拟) 把菱形按照如图所示的规律拼图案，其中第①个图案中有 1个菱形，第②个图案中有 3个菱形，第③个图案中有5个菱形，…，按此规律排列下去，则第⑥个图案中菱形的个数为（）

A . 15 B . 13 C . 11 D . 9

答案解析收藏纠错 + 选题
7. (2024九下·西吉期末) 估计 $\text{[math]}$ 的值在（）

A . 6 到 7 之间 B . 5 到 6 之间 C . 4 到 5 之间 D . 3 到 4 之间

答案解析收藏纠错 + 选题
8. 学校连续三年组织学生参加义务植树，第一年共植树 400 棵，第三年共植树 625 棵．设该校植树棵数的年平均增长率为 x，根据题意，下列方程正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2023八下·杭州期中) 如图，在正方形 ABCD 中，对角线 AC，BD 相交于点 O．E，F 分别为 AC，BD 上一点，且 OE=OF，连接 AF，BE，EF，若∠AFE=25°，则∠CBE 的度数为（）

A . 50° B . 55° C . 65° D . 70°

答案解析收藏纠错 + 选题
10. (2022·重庆) 如图，AB是⊙O的直径，C为 ⊙O上一点，过点 C的切线与 AB 的延长线交于点 P，若 AC=PC= $\text{[math]}$ ，则 PB 的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 3

答案解析收藏纠错 + 选题
11. (2023八上·金乡县期末) 关于x的分式方程 $\text{[math]}$ 的解为正数，且关于y的不等式组 $\text{[math]}$ 的解集为y≥5，则所有满足条件的整数a的值之和是（）

A . 13 B . 15 C . 18 D . 20

答案解析收藏纠错 + 选题
12. (2022·重庆) 对多项式x-y-z-m-n任意加括号后仍然只含减法运算并将所得式子化简，称之为“加算操作”，例如：(x-y)-(z-m-n)=x-y-z+m+n，x-y-(z-m)-n = x-y-z+m-n，……，
给出下列说法：

①至少存在一种“加算操作”，使其结果与原多项式相等； ②不存在任何“加算操作”，使其结果与原多项式之和为0； ③所有的“加算操作”共有 8 种不同的结果．以上说法中正确的个数为（）

A . 0 B . 1 C . 2 D . 3

答案解析收藏纠错 + 选题

二、填空题（共4个小题，每小题4分，共16分）

13. (2023八下·江北月考) $\text{[math]}$ =．

答案解析收藏纠错 + 选题
14. (2022·重庆) 在不透明的口袋中装有2个红球，1个白球，它们除颜色外无其他差别，从口袋中随机摸出一个球后，放回并摇匀，再随机摸出一个球，两次摸出的球都是红球的概率为．

答案解析收藏纠错 + 选题
15. (2022·重庆) 如图，在矩形 ABCD中， AB=1，BC=2，以B为圆心，BC 的长为半轻画弧，交 AD 于点 E．则图中阴影部分的面积为．(结果保留 π)

答案解析收藏纠错 + 选题
16. (2022·重庆) 特产专卖店销售桃片、米花糖、麻花三种特产，其中每包桃片的成本是麻花的 2 倍，每包桃片、米花糖、麻花的售价分别比其成本高 20%、30%、20%．该店五月份销售桃片、米花糖、麻花的数量之比为 1：3：2，三种特产的总利润是总成本的 25%，则每包米花糖与每包麻花的成本之比为．

答案解析收藏纠错 + 选题

三、解答题（共2个小题，每小题8分，共16分）

17. (2022·重庆) 计算：
1. （1） (x+ y)(x-y)+y(y-2)
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
18. (2022·重庆) 我们知道，矩形的面积等于这个矩形的长乘宽，小明想用其验证一个底为 a，高为 h 的三角形的面积公式为 $\text{[math]}$ . 想法是：以 BC 为边作矩形 BCFE，点 A 在边FE上，再过点 A 作 BC 的垂线，将其转化为证三角形全等，由全等图形面积相等来得到验证．按以上思路完成下面的作图与填空

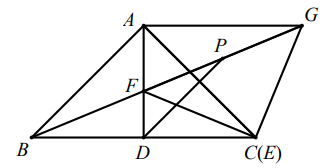
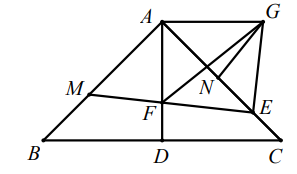
证明：用直尺和圆规过点 A 作 BC 的垂线 AD 交 BC 于点 D．(只保留作图痕迹)

在△ADC 和△CFA 中，

∵AD⊥BC

∴∠ADC=90° .

∴∠F= 90°，

∴    ①

∵EF∥ BC，

∴   ②

又∵    ③

∴△ADC≌△CFA (AAS).

同理可得： ④

$\text{[math]}$ .

答案解析收藏纠错 + 选题

四、解答题（共7个小题，每小题10分，共70分）

19. (2022·重庆) 在“世界读书日”到来之际，学校开展了课外阅读主题周活动，活动结束后，经初步统计，所有学生的课外阅读时长都不低于 6 小时，但不足 12 小时，从七，八年级中各随机抽取了 20 名学生，对他们在活动期间课外阅读时长(单位：小时)进行整理、描述和分析(阅读时长记为 x，6≤x<7，记为 6；7≤x<8，记为 7；8≤x<9，记为 8；...以此类推)，下面分别给出了抽取的学生课外阅读时长的部分信息，

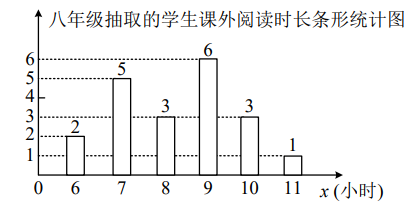
七年级抽取的学生课外阅读时长：

6，7，7，7，7，8，8，8，8，8，8，8，9，9，9，9，9，10，10，11，

七，八年级抽取的学生课外阅读时长统计表
年级	七年级	八年级
平均数	8.3	8.3
众数	a	9
中位数	8	b
8小时及以上所占百分比	75%	c

根据以上信息，解答下列问题：

（1）填空： a = ， b =， c = ．
（2）该校七年级有 400 名学生，估计七年级在主题周活动期间课外阅读时长在 9 小时及以上的学生人数．
（3）根据以上数据，你认为该校七，八年级学生在主题周活动中，哪个年级学生的阅读积极性更高?请说明理由，（写出一条理由即可）

答案解析收藏纠错 + 选题

20. (2022·重庆) 反比例函数 $\text{[math]}$ 的图象如图所示，一次函数 y=kx+b(k≠0)的图象与 $\text{[math]}$ 的图象交于A (m， 4)，B(-2，n)两点，
1. （1）求一次函数的表达式，并在所给的平面直角坐标系中面出该函数的图象；
2. （2）观察图象，直接写出不等式 $\text{[math]}$ 的解集；
3. （3）一次函数y=kx+b的图象与 x 轴交于点 C，连接 OA，求△OAC 的面积．
答案解析收藏纠错 + 选题
21. (2022·重庆) 为保障蔬菜基地种植用水，需要修建灌溉水渠．
1. （1）计划修建灌溉水渠600米，甲施工队施工5天后，增加施工人员，每天比原来多修建20米，再施工2天完成任务，求甲施工队增加人员后每天修建灌溉水渠多少米？
2. （2）因基地面积扩大，现还需修建另一条灌溉水渠1800米，为早日完成任务，决定派乙施工队与甲施工队同时开工合作修建这条水渠，直至完工．甲施工队按（1）中增加人员后的修建速度进行施工．乙施工队修建 360 米后，通过技术更新，每天比原来多修建 20%，灌溉水渠完工时，两施工队修建的长度恰好相同．求乙施工队原来每天修建灌溉水渠多少米？
答案解析收藏纠错 + 选题
22. (2022·重庆) 湖中小岛上码头C处一名游客突发疾病，需要救援．位于湖面B点处的快艇和湖岸 A处的救援船接到通知后立刻同时出发前往救援．计划由快艇赶到码头 C 接该游客，再沿 CA方向行驶，与救援船相遇后将该游客转运到救援船上．已知 C 在A的北偏东 30°方向上，B在A的北偏东 60°方向上，且在C的正南方向 900米处．
1. （1）求湖岸 A 与码头 C 的距离（结果精确到 1 米，参考数据： $\text{[math]}$ =1.732 ）；
2. （2）救援船的平均速度为 150 米/分，快艇的平均速度为 400 米/分，在接到通知后，快艇能否在5分钟内将该游客送上救援船？请说明理由．（接送游客上下船的时间忽略不计）
答案解析收藏纠错 + 选题
23. (2022·重庆) 对于一个各数位上的数字均不为 0 的三位自然数 N，若 N 能被它的各数位上的数字之和 m 整除，则称 N 是 m 的“和倍数”．
例如：∵247÷(2+4+7)= 247÷13=19，∴247是13的“和倍数”.

又如： ∵214÷(2+1+4)=214÷7=30……4，∴214不是“和倍数”.
1. （1）判断 357，441 是否是“和倍数”？说明理由；
2. （2）三位数 A是12的“和倍数”，a，b，c 分别是数 A其中一个数位上的数字，且 a>b>c在 a，b，c 中任选两个组成两位数，其中最大的两位数记为 F (A)，最小的两位数记为 G(A)，若 $\text{[math]}$ 为整数，求出满足条件的所有数 A．
答案解析收藏纠错 + 选题
24. (2022·重庆) 如图，在平面直角坐标系中，抛物线 $\text{[math]}$ 与x轴交于点 A(4，0)，与 y 轴交于点 B(0，3)．
1. （1）求抛物线的函数表达式；
2. （2）点 P为直线AB上方抛物线上一动点，过点P作 PQ⊥x 轴于点Q，交 AB于点 M，求 $\text{[math]}$ 的最大值及此时点 P 的坐标；
3. （3）在（2）的条件下，点 P' 与点P关于抛物线 $\text{[math]}$ 的对称轴对称．将抛物线 $\text{[math]}$ 向右平移，使新抛物线的对称轴l经过点A．点 C 在新抛物线上，点D在l上，直接写出所有使得以点 A、P'、C、D为顶点的四边形是平行四边形的点 D 的坐标，并把求其中一个点D的坐标的过程写出来．
答案解析收藏纠错 + 选题
25. (2022·重庆) 在△ ABC中，∠BAC=90° ，AB=AC= $\text{[math]}$ ，D为 BC的中点，E，F分别为AC， AD 上任意一点，连接EF，将线段EF绕点E顺时针旋转 90°得到线段EG，连接FG， AG．
1. （1）如图1，点 E 与点 C 重合，且 GF 的延长线过点 B ，若点 P 为 FG 的中点，连接 PD，求 PD的长；
2. （2）如图 2，EF 的延长线交 AB 于点M，点N在 AC上， ∠AGN=∠AEG 且GN=MF，求证：AM+AF= $\text{[math]}$ AE
3. （3）如图3，F为线段 AD上一动点，E为 AC的中点，连接BE，H为直线BC上一动点，连接 EH，将△ BEH沿EH翻折至△ABC所在平面内，得到△ B'EH'，连接 B'G，直接写出线段 B'G的长度的最小值
答案解析收藏纠错 + 选题