江苏省泰兴市2021-2022学年八年级下学期期末学业质量监...

更新时间：2024-07-13 浏览次数：71 类型：期末考试

一、选择题（本大题共6小题，每小题3分，共18分，）

1. (2022八下·泰兴期末) 江苏省第二十届运动会将于今年8月28日在泰州举行，运动会会徽依据“江苏•泰州”首字母为原型进行设计．下列字母中，是中心对称图形的有（）个．

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
2. (2022八下·泰兴期末) 若关于x的方程（a﹣1）x²＝2为一元二次方程，则a满足（）

A . a＝1 B . a≠1 C . a＝0 D . a≠0

答案解析收藏纠错 + 选题
3. (2024八下·姜堰期末) 下列是最简二次根式的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2022八下·泰兴期末) 如图，在平行四边形ABCD中，AC，BD相交于点O，BD⊥AD，AC＝10cm，BC＝4cm，则BD的长为（）

A . 4cm B . 5cm C . 6cm D . 8cm

答案解析收藏纠错 + 选题
5. (2022八下·泰兴期末) 已知反比例函数y＝ $\text{[math]}$ ，当﹣2＜x＜﹣1时，y的取值范围为（）

A . ﹣10＜y＜﹣5 B . ﹣2＜y＜﹣1 C . y＞﹣5 D . y＜﹣10

答案解析收藏纠错 + 选题
6. (2022八下·泰兴期末) 某超市销售一批玩具，平均每天可售出120件，每件盈利4元，市场调查发现售价每涨1元，销售量减少10件；售价每降1元，销售量增加10件。爱动脑的嘉嘉发现：在一定范围内，涨a元与降b元所获得的利润相同，则a与b满足（）

A . a﹣b＝4 B . a﹣b＝8 C . a+b＝4 D . a+b＝8

答案解析收藏纠错 + 选题

二、填空题（本大题共10小题，每小题3分，共30分。）

7. (2022八下·泰兴期末) 若 $\text{[math]}$ 有意义，则x的取值范围是．

答案解析收藏纠错 + 选题
8. (2022八下·泰兴期末) “14人中至少有2人在同一个月过生日”这一事件是事件．（填“必然”、“不可能”或“随机”）

答案解析收藏纠错 + 选题
9. (2022八下·泰兴期末) 在矩形ABCD中，对角线AC、BD相交于点O，AO＝6cm，则BD＝cm．

答案解析收藏纠错 + 选题
10. (2024七下·凉州期末) 比较大小： $\text{[math]}$ $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2022八下·泰兴期末) 关于x的方程x²+2x﹣4＝0的两根为x₁、x₂ ，则x₁﹣x₁•x₂+x₂＝．

答案解析收藏纠错 + 选题
12. (2022八下·泰兴期末) 如图，点A是反比例函数y＝ $\text{[math]}$ 图象上一点，过点A分别作x轴，y轴的垂线，垂足为B，C，则四边形ABOC的面积为．

答案解析收藏纠错 + 选题
13. (2022八下·泰兴期末) 如图，菱形ABCD中，对角线AC与BD交于点O，OE⊥AB，∠ADC＝α，则∠AOE＝．（用含α的式子表示）

答案解析收藏纠错 + 选题

14. (2022八下·泰兴期末) 某批排球的质量检验结果如下：

抽取的篮球数n	50	200	400	600	800	1000	1200
优等品的频数m	46	186	372	561	744	931	1116
优等品的频率 $\text{[math]}$	0.92	0.930	0.930	0.935	0.930	0.931	0.930

从这批排球中，任意抽取的一个排球是优等品的概率的估计值是．（精确到0.01）

答案解析收藏纠错 + 选题

15. (2022八下·泰兴期末) 已知A（m，y₁）、B（m+3，y₂）是反比例函数y＝ $\text{[math]}$ 图象上两点，且y₁﹣y₂＜0，则m的取值范围为．

答案解析收藏纠错 + 选题
16. (2022八下·泰兴期末) 如图，正方形ABCD中，AB＝4，BE＝CE，F是边AB上一动点，连接EF，翻折△BEF至△GEF，使得B落在G处，连接DG，当四边形AFGD的周长取得最小值时，则BF＝．

答案解析收藏纠错 + 选题

三、解答题（本大题共10小题，共102分。）

17. (2023九上·福田期中) 解方程：
1. （1） x（x+2）＝2（x+2）；
2. （2） 3x²﹣x﹣1＝0．
答案解析收藏纠错 + 选题
18. (2022八下·泰兴期末) 计算：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
19. (2022八下·泰兴期末) 今年是中国共青团成立100周年，我市某中学团委开展了“永远跟党走，喜迎二十大”主题教育活动．为了了解这次宣传活动的效果，学校从全校1200名学生中随机抽取了部分学生进行知识测试，并将测试成绩分为A，B，C，D，E五个等级，绘制成了统计图．
1. （1）求扇形统计图中“B”所对应的圆心角的度数．
2. （2）对于这次调查，下列推断合理的序号是；
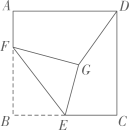
  ①调查的样本容量是1200；
  
  ②个体是每个学生的知识测试等级
  
  ③条形统计图中“D”等级的人数超过“A”等级的人数的一半；
  
  ④扇形统计图主要用于表示总体中各部分所占的百分比．
3. （3）如果测试成绩为A、B等级的均为优秀，请估计该校成绩优秀的学生人数
答案解析收藏纠错 + 选题
20. (2022八下·泰兴期末) 如图，四边形ABCD为平行四边形，O是DC的中点，连接BO并延长交AD的延长线于点E，且AB＝BE．
求证：四边形CBDE是矩形．

答案解析收藏纠错 + 选题
21. (2022八下·泰兴期末) 某商店5月份的利润为20000元，6月份的利润比5月份增加25%．要使8月份的利润达到36000元，则6至8月份平均每月利润增长的百分率是多少？

答案解析收藏纠错 + 选题
22. (2022八下·泰兴期末) 如图，△ABC中，AB＝AC＝5，BC＝6．
1. （1）仅用圆规在平面内找一点D（异于点A），使得点D到射线AB、AC的距离相等，且DB＝5；（不写作法，保留作图痕迹）
2. （2）求四边形ABDC的面积．
答案解析收藏纠错 + 选题
23. (2022八下·泰兴期末) 如图，一次函数y₁＝kx+2的图象与反比例函数y₂＝﹣ $\text{[math]}$ 的图象相交于A（a，﹣2a）、B（4，﹣2）．
1. （1）求a、k的值；
2. （2）结合图象，直接写出不等式kx+2+ $\text{[math]}$ ＜0的解集：
3. （3）连接OA、OB，求△AOB的面积．
答案解析收藏纠错 + 选题
24. (2022八下·泰兴期末) 【阅读理解】我们把b²﹣4ac叫做一元二次方程ax²+bx+c＝0（a≠0）根的判别式．当一元二次方程ax²+bx+c＝0（a≠0）有实数根时，判别式b²﹣4ac≥0，即得到一个关于a、b、c的不等关系式．我们把利用判别式解决问题的方法叫做判别式法．
【例题示范】例：已知关于x的方程2x²﹣3x+c＝0有实数根，求c的取值范围．

解：一元二次方程有实数根的条件是b²﹣4ac≥0，即（﹣3）²﹣4×2c≥0，解得c≤ $\text{[math]}$

【问题解决】
1. （1）关于x的方程 $\text{[math]}$ x²+（t+2）x+t²+4＝0有实数根，求t的值或取值范围
2. （2）用一段长16cm的铁丝围成一个矩形，设矩形的长是xcm，面积是Scm² ．
  ①用x的代数式表示S，并将此等式整理成关于x的一元二次方程的一般形式；
  ②请运用判别式法求S的最大值，并求出此时x的值．
答案解析收藏纠错 + 选题
25. (2022八下·泰兴期末) 如图1，D、E、F分别是△ABC各边上的点，四边形ADEF是平行四边形，有三个选项：①D是AB的中点，②E是BC的中点，③F是AC的中点．
1. （1）请从三个选项中选择两个作为条件，余下一个作为结论，并证明．
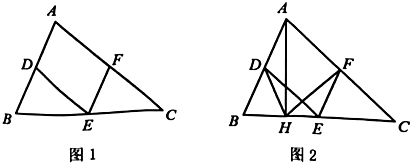
  你选择的条件是 ▲ ，结论是 ▲ （填序号）；
2. （2）在（1）的条件下，如图2，点H在BC上，AH⊥BC，连接DH、FH，
  ①若∠B+∠C＝100°，求∠DHF的度数；
  
  ②若AB＝8，AC＝10，连接DF，△DHF的面积为S，直接写出S的取值范围．
答案解析收藏纠错 + 选题
26. (2022八下·泰兴期末) 如图1，在平面直角坐标系中，点A（﹣1，2）绕原点顺时针旋转90°至点B，恰好落在反比例函数y＝ $\text{[math]}$ 的图象上，连接OA，OB，过点B作BC⊥x轴交于点C，点P（m，n）是第一象限内双曲线上一动点．
1. （1）求反比例函数的解析式；
2. （2）若S_△_POC＝4S_△_PBC ，求P的坐标；
3. （3）如图2，连接PO并延长交双曲线于G（﹣m，﹣n），平面内有一点Q（m﹣1，n+2），PQ与GA的延长线交于点H；
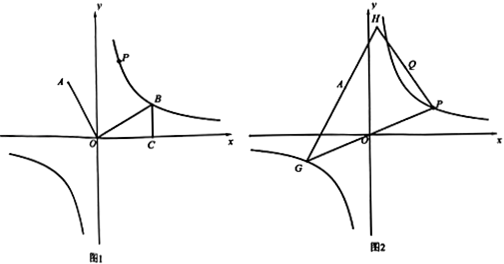
  ①若m＝2，求点H的坐标；
  ②当m≠1时，记H的坐标为（a，b），试判断（a+2）（b﹣4）是否为定值？若为定值，求出该值；若不为定值，说明理由．
答案解析收藏纠错 + 选题