浙江省绍兴市新昌县2021-2022学年八年级下学期期末检测...

更新时间：2024-07-13 浏览次数：109 类型：期末考试

一、选择题（本大题共有10小题，每小题3分，共30分．请选出每小题中一个最符合题意的选项，不选、多选、错选均不给分）

1. (2023八下·潮南期中) 二次根式 $\text{[math]}$ 中字母x的取值可以是（）

A . x＝0 B . x＝1 C . x＝2 D . x＝5

答案解析收藏纠错 + 选题
2. (2022八下·新昌期末) 下列图形是以数学家名字命名的，其中属于中心对称图形的是（）．

A . 笛卡尔心形线 B . 赵爽弦图 C . 菜洛三角形 D . 斐波那契螺旋线

答案解析收藏纠错 + 选题
3. (2022八下·新昌期末) 下列各点落在反比例函数y= $\text{[math]}$ 图象上的是（）

A . （-4，1） B . （-1，4） C . （2，2） D . （-2，2）

答案解析收藏纠错 + 选题
4. (2022八下·新昌期末) 下列各式计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2022八下·新昌期末) 如图，在同一平面内，将边长相等的正六边形、正方形的一边重合，则∠1的度数为（）

A . 18° B . 25° C . 30° D . 45°

答案解析收藏纠错 + 选题
6. (2022八下·新昌期末) 若关于x的一元二次方程kx²+2x-1=0有实数根，则k的取值范围是（）

A . k>-1 B . k>-1且k≠0 C . k≥-1 D . k≥-1且k≠0

答案解析收藏纠错 + 选题
7. (2022八下·新昌期末) 要说明命题“多边形的内角和一定不小于其外角和”是假命题，可选择的反例是（）

A . 三角形 B . 菱形 C . 矩形 D . 八边形

答案解析收藏纠错 + 选题
8. (2024八下·东阳期中) 2021 年，党中央国务院赋予浙江省建设“共同富裕示范区”的光荣使命，共同富裕的要求是：在消除两极分化和贫穷基础上实现普遍富裕．下列有关人均收入的统计量特征中，最能体现共同富裕要求的是（）

A . 平均数大，方差大 B . 平均数大，方差小 C . 平均数小，方差小 D . 平均数小，方差大

答案解析收藏纠错 + 选题
9. (2022八下·新昌期末) 如图，一块长方形绿地长10m，宽5m．在绿地中开辟三条道路后，绿地面积缩小到原来的78%，则可列方程为（）

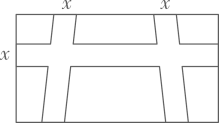
A . （10-2x）（5-x）=10×5×78% B . （10-2x）（5-x）+2x²=10×5×78% C . （10-2x）（5+x）=10×5×78% D . （10-2x）（5-x）-2x²=10×5×78%

答案解析收藏纠错 + 选题
10. (2022八下·新昌期末) 如图在边长为1的小正方形构成的5×4的网格中，定义：以网格中的格点为顶点的正方形叫做格点正方形．则图中完全包含“”的格点正方形最多能画（）

A . 13个 B . 16个 C . 19个 D . 21个

答案解析收藏纠错 + 选题

二、填空题（本大题共有6小题，每小题3分，共18分．）

11. (2022八下·新昌期末) 计算 $\text{[math]}$ 的结果是

答案解析收藏纠错 + 选题
12. (2022八下·新昌期末) 点P（3，-2）关于原点对称的点的坐标是．

答案解析收藏纠错 + 选题
13. (2022八下·新昌期末) 一元二次方程x²+bx -2023=0的一个根为x=1，则b的值为．

答案解析收藏纠错 + 选题
14. (2022八下·新昌期末) 如图，在矩形ABCD中，AB：BC=3：4，BP=3，将OABP沿AP翻折，点B恰好落在对角线AC上的点E处，则BC的长为

答案解析收藏纠错 + 选题
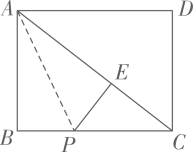
15. (2024九上·扶余期末) 如图，函数y= $\text{[math]}$ （x>0）的图象过矩形OBCD一边的中点，且图象过矩形OAPE的顶点P，若阴影部分面积为6，则k的值为

答案解析收藏纠错 + 选题
16. (2022八下·新昌期末) 如图，正方形ABCD边长为2，点E，F是对角线AC上的动点，且EF长度为1，连结BE，BF，则△BEF周长的最小值为

答案解析收藏纠错 + 选题

三、解答题（本大题共8小题，第17~18题每题5分，第19~22题每题6分，第23题8分，第24题10分，共52分．解答衢写出必要的文字说明、演算步骤或证明过程）

17. (2022八下·新昌期末) 计算：
1. （1） $\text{[math]}$
2. （2）（ $\text{[math]}$ +1）（ $\text{[math]}$ -1）
答案解析收藏纠错 + 选题
18. (2022八下·新昌期末) 解方程：
1. （1） x²=9
2. （2） x²+2x-3=0
答案解析收藏纠错 + 选题
19. (2022八下·新昌期末) 如图是由边长为1的小正方形构成的6×4的网格，点A，B均在格点上。
1. （1）在图1中画出以AB为边的平行四边形，且顶点均在格点上（画出一个即可）
2. （2）在图2中画出以AB为对角线的正方形，且顶点均在格点上．
答案解析收藏纠错 + 选题
20. (2022八下·新昌期末) 某社区为了增强居民节约用水的意识，随机调查了部分家庭2021年的月均用水量（单位：t）．根据调查结果，绘制出如下的统计图1和图2．

请根据相关信息，解答下列问题：
1. （1）这组月均用水量数据的众数为吨，中位数为吨．
2. （2）求m的值．
答案解析收藏纠错 + 选题
21. 如图，在 $\text{[math]}$ ABCD中，对角线AC，BD相交于点O，AC⊥BC，延长BC至点E，使BC=CE，连结DE．
1. （1）求证：四边形ACED是矩形．
2. （2）若BC=3，AB=5，求BD的长．
答案解析收藏纠错 + 选题
22. (2022八下·新昌期末) 请根据图片内容，回答下列问题：

我叫Omicron（奥密克戎），是新冠病毒的变异毒株，我的传染性很强，传播速度很快。有一次我感染了1个人，此人未被有效隔离，经过两轮传染后共有121名感染者．
1. （1）每轮传染中，平均一个人传染了几个人？
2. （2）按照这样的速度传染，第三轮将新增多少名感染者（假设每轮传染人数相同）？
答案解析收藏纠错 + 选题
23. (2022八下·新昌期末) 如图，已知反比例函数y= $\text{[math]}$ （k≠0）与正比例函数y=2x的图象交于A（1，m），B两点．
1. （1）求该反比例函数的表达式．
2. （2）当 $\text{[math]}$ ≥2x时，请结合图象直接写出x的取值范围．
3. （3）若点Q在x轴上，点P在双曲线上，当A，B，P，Q为顶点的四边形是平行四边形时，求此时点P的坐标．
答案解析收藏纠错 + 选题
24. (2022八下·新昌期末) 如图，在菱形ABCD中，AD=4，∠ADC=60°，点E是AD边上的中点，点F是对角线BD上一动点，连结EF．
1. （1）若EF⊥BD，求DF的长．
2. （2）作点D关于直线EF的对称点P，直线PE与对角线BD交于点Q．
  ①若点F为BD中点，求PQ的长．
  
  ②在点F的运动过程中，△DEQ的面积可能为 $\text{[math]}$ 吗？若可能，求出此时DF的长，若不可能，请说明理由．
答案解析收藏纠错 + 选题