湖北省武汉市青山区2021-2022学年七年级下学期期中数学...

更新时间：2022-09-09 浏览次数：168 类型：期中考试

一、单选题

1. (2023七下·江阴期中) 如图所示的图案分别是大众、奥迪、奔驰、三菱汽车的车标，其中，可以看作由“基本图案”经过平移得到的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2022七下·青山期中) 在平面直角坐标系中，点A（2，﹣3）位于（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
3. (2024八上·秦安月考) 4的算术平方根是（）

A . -2 B . 2 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2022七下·青山期中) 在3.14， $\text{[math]}$ ，－ $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， 1.01001000100001这六个数中，无理数有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
5. (2022七下·青山期中) 如图，直线a，b被直线c所截，下列条件中，不能判定a∥b（）

A . ∠2=∠4 B . ∠1+∠4=180° C . ∠5=∠4 D . ∠1=∠3

答案解析收藏纠错 + 选题
6. (2023七下·大冶期中) 下列各式错误的是（）

A . $\text{[math]}$ ＝2 B . $\text{[math]}$ ＝－0.1 C . $\text{[math]}$ ＝±2 D . $\text{[math]}$ ＝－ $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024七下·科尔沁左翼中旗期中) 已知A点的坐标为（3，a＋3），B点的坐标为（a，4），AB∥x轴，则线段AB的长为（）

A . 5 B . 4 C . 3 D . 2

答案解析收藏纠错 + 选题
8. (2022七下·青山期中) 如图，将一张长方形纸片按如图所示的方式沿虚线折叠，得到两个面积分别为16和5的正方形，则阴影部分的面积为（）

A . 4 $\text{[math]}$ －5 B . 3 $\text{[math]}$ C . 4－ $\text{[math]}$ D . 4＋ $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2022七下·麻章期末) 下列命题中，真命题的个数有（）
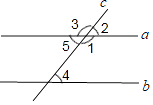
①同旁内角互补：②两个无理数的和一定是无理数：③±4是64的立方根：④过一点有且只有一条直线与已知直线平行．

A . 0个 B . 1个 C . 2个 D . 3个

答案解析收藏纠错 + 选题
10. (2023七下·大冶期中) 如图，长为50m，宽为30m的长方形地块上，有纵横交错的几条小路，宽均为1m，其它部分均种植草坪，则种植草坪的面积为（）

A . 1344m² B . 1421m² C . 1431m² D . 1341m²

答案解析收藏纠错 + 选题

二、填空题

11. (2024七下·湘西期中) 实数－ $\text{[math]}$ 的相反数是．

答案解析收藏纠错 + 选题
12. (2022七下·青山期中) 已知点P（x＋2，2x－3）在y轴上，则x＝．

答案解析收藏纠错 + 选题
13. (2022七下·青山期中) 若一个数的平方根就是它本身，则这个数是．

答案解析收藏纠错 + 选题
14. (2022七下·青山期中) 如图，一条公路两次转弯后，和原来的方向相同．如果第一次的拐角∠A的度数为130°，第二次拐角∠B的度数为．

答案解析收藏纠错 + 选题
15. (2023九上·深圳月考) 如图，在平面直角坐标系中，点A在x轴上，点B（0，9），线段AB向右平移3个单位至线段CD，线段CD与y轴交于点E，若图中阴影部分面积是21，则点C的坐标为．

答案解析收藏纠错 + 选题
16. (2022七下·青山期中) 如图，已知AB∥CD，E、F、H分别为AB、CD、AC上一点（∠DFK＜∠BEK），KG平分∠EKF，∠AEK＋∠HKE＝180°．则下列结论：①CD∥KH；②∠BEK＋∠DFK＝2∠EKG；③∠BEK－∠DFK＝∠GKH；④∠BAC＋∠AGK－∠GKF＋∠DFK＝180°．其中正确的是．（填序号）

答案解析收藏纠错 + 选题

三、解答题

17. (2022七下·青山期中) 计算：
1. （1） $\text{[math]}$ － $\text{[math]}$ ；
2. （2） | $\text{[math]}$ － $\text{[math]}$ |＋2 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
18. (2022七下·青山期中) 解方程：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
19. (2022七下·青山期中) 请根据条件进行推理，得出结论，并在括号内注明理由．
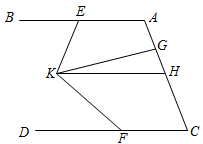
已知：如图，∠1＝∠2，∠B＋∠CDE＝180°．

求证：AB∥CD．

证明：∵∠1＝   （    ）

又∵∠1＝∠2

∴∠BFD＝∠2（   ）

∴BC∥   （    ）

∴∠C＋＝180°（    ）

又∵∠B＋∠CDB＝180°

∴∠B＝∠C

∴AB∥CD（    ）．

答案解析收藏纠错 + 选题
20. (2022七下·青山期中) 如图，直线EF、CD相交于点O，OA⊥OB，OC平分∠AOF．
1. （1）直接写出∠DOF的对顶角和邻补角；
2. （2）若∠AOE＝30°，求∠BOD的度数．
答案解析收藏纠错 + 选题
21. (2022七下·青山期中) 如图，在边长为1个单位长度的小正方形组成的网格中，△ABC的顶点均在格点上．
1. （1）请建立合适的平面直角坐标系，使点A，点B的坐标分别为A（－1，3）、B（3，1），并写出点C的坐标；
2. （2）在（1）的条件下．
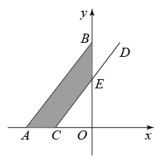
  ①若△ABC中任意一点P（a，b）平移后对应点为P（a＋2，b－5），将△ABC作同样的平移得到△A₁B₁C₁ ．请画出平移后的△A₁B₁C₁；
  ②点Q为y轴上一动点，当AQ＋BQ最小时，直接写出点Q的坐标．
答案解析收藏纠错 + 选题
22. (2022七下·青山期中) 某小区有一个由实木栅栏围成的400m²的正方形室外阅读场地，现在要将其改建成300m²的长方形场地，且长和宽之比为3：2．
1. （1）求这个长方形场地的长宽分别是多少m？
2. （2）如果要把原来围成正方形场地的实木栅栏利用起来，围成这个长方形场地，那么这些实木栅栏是否够用？并说明理由．
答案解析收藏纠错 + 选题
23. (2024七下·夷陵期中) 已知，直线AB∥CD，点E、F分别在直线AB、CD上，点P是直线AB与CD外一点，连接PE、PF．
1. （1）如图1，若∠AEP＝45°，∠DFP＝105°，求∠EPF的度数：
2. （2）如图2，过点E作∠AEP的角平分线EM交FP的延长线于点M，∠DFP的角平分线FN交EM的反向延长线于点N，若∠M与3∠N互补，试探索直线EP与直线FN的位置关系，并说明理由；
3. （3）若点P在直线AB的上方且不在直线EF上，作∠DFP的角平分线FN交∠AEP的角平分线EM所在直线于点N，请直接写出∠EPF与∠ENF的数量关系．
答案解析收藏纠错 + 选题
24. (2022七下·青山期中) 已知，点A在y轴正半轴上，OA＝a，点B位于第二象限，且点B到两坐标轴的距离均为b，其中a、b满足b＝ $\text{[math]}$ ＋ $\text{[math]}$ ＋4．
1. （1） a＝，b＝；
2. （2）点C在x轴的负半轴上，射线CD∥AB．
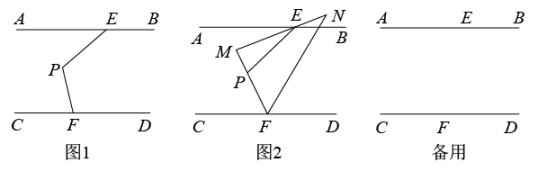
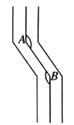
  ①如图1，过C作射线CE交y轴于点E，使∠DCE＝3∠ECO，过A作射线AF交CE于点F，使∠BAF＝3∠OAF，求∠AFE的度数；
  ②如图2，设点C的坐标为（m，0），射线CD上点P的坐标为（n，1），试探索m与n的数量关系，并说明理由．
答案解析收藏纠错 + 选题