 B .
C .
B .
C .  D .
D . 

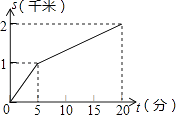 B .
B . 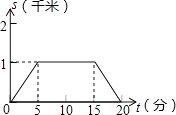 C .
C . 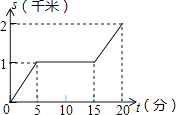 D .
D . 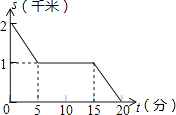












碗的数量x(个) | 1 | 2 | 3 | 4 | 5 | … |
高度y(cm) | 4 | 5.2 | 7.6 | … |

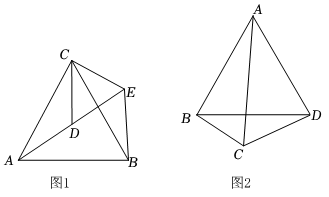
学生经过讨论,探究出以下解决问题的思路:
思路一:延长CB到E,使BE=CD,连接AE,证得△ABE≌△ADC,从而容易证明△ACE是等边三角形,故AC=CE,等量代换得到AC=BC+CD.
思路二:将△ABC绕着点A逆时针旋转60°至△ADF,从而容易证明△ACF是等边三角形,故AC=CF,等量代换得到AC=BC+CD.
请选择一种思路,作出图形并写出证明过程.
