安徽省蚌埠市2021-2022学年高三上学期理数第二次教学质...

更新时间：2022-09-15 浏览次数：43 类型：期末考试

一、单选题

1. (2022高三上·蚌埠期末) 已知集合 $\text{[math]}$ ，集合 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022高三上·蚌埠期末) 设复数 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . 1 B . -1 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2022高三上·蚌埠期末) 《数书九章》是我国宋代数学家秦九韶的著作，其中给出了求多项式值的秦九韶算法，如图所示的程序框图给出了一个利用秦九韶算法求某多项式值的实例．若输入的 $\text{[math]}$ ，则输出的y值是（）

A . 2 B . 16 C . 32 D . 64

答案解析收藏纠错 + 选题
4. (2022高三上·蚌埠期末) 已知 $\text{[math]}$ ， $\text{[math]}$ 为锐角， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2022高三上·蚌埠期末) 已知双曲线 $\text{[math]}$ （ $\text{[math]}$ ）的左､右焦点分别为 $\text{[math]}$ ， $\text{[math]}$ ，过点 $\text{[math]}$ 作一条渐近线的垂线，垂足为P若 $\text{[math]}$ 的面积为 $\text{[math]}$ ，则该双曲线的离心率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 3 D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022高三上·蚌埠期末) 某市有 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 五所学校参加中学生体质抽测挑战赛，决出第一名到第五名的名次． $\text{[math]}$ 校领导和 $\text{[math]}$ 校领导去询问成绩，回答者对 $\text{[math]}$ 校领导说：“很遗憾，你和 $\text{[math]}$ 校都没有得到第一名”，对 $\text{[math]}$ 校领导说“你也不是最后一名”．从这两个回答分析，这五个学校的名次排列的不同情况共有（）

A . 27种 B . 36种 C . 54种 D . 72种

答案解析收藏纠错 + 选题
7. (2022高三上·蚌埠期末) 函数 $\text{[math]}$ 的图象大致为（）

A . B . C . D .

答案解析收藏纠错 + 选题
8. (2022高三上·蚌埠期末) 将函数 $\text{[math]}$ 的图象向右平移 $\text{[math]}$ 个单位长度后得到函数 $\text{[math]}$ 的图象，则函数 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2022高三上·蚌埠期末) 若正实数x，y满足 $\text{[math]}$ ．则 $\text{[math]}$ 的值不可能是（）

A . 12 B . 9 C . 6 D . 3

答案解析收藏纠错 + 选题
10. (2022高三上·蚌埠期末) 如图，正方体 $\text{[math]}$ 中，点Q为 $\text{[math]}$ 的中点，点N为 $\text{[math]}$ 的中点．有下列四个结论：
① $\text{[math]}$ 平面 $\text{[math]}$ ；② $\text{[math]}$ 平面 $\text{[math]}$ ；③ $\text{[math]}$ ；④异面直线BN与CD所成角为45°．
其中正确的结论有（）

A . ①② B . ①③ C . ②④ D . ①④

答案解析收藏纠错 + 选题
11. (2022高三上·蚌埠期末) 已知向量 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的最大值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2022高三上·蚌埠期末) 已知函数 $\text{[math]}$ ，设 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则a，b，c的大小关系为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

13. (2022高三上·蚌埠期末) 设抛物线 $\text{[math]}$ 上一点 $\text{[math]}$ 到 $\text{[math]}$ 轴的距离是到焦点距离的一半，则抛物线的标准方程为．

答案解析收藏纠错 + 选题
14. (2022高三上·玉溪月考) 某单位为了制定节能减排的目标，先调查了用电量y（度）与气温x（℃）之间的关系，随机统计了某4天的用电量与当天气温，并制作了对照表：
气温（℃）
18
13
10
－1
用电量（度）
24
34
38
64
由表中数据，得线性回归方程 $\text{[math]}$ ，当气温为－5℃时，预测用电量的度数约为．

答案解析收藏纠错 + 选题
15. (2022高三上·蚌埠期末) 已知定义域为 $\text{[math]}$ 的函数 $\text{[math]}$ 的图象关于 $\text{[math]}$ 轴对称，且满足 $\text{[math]}$ ．若曲线 $\text{[math]}$ 在 $\text{[math]}$ 处切线的斜率为4，则曲线 $\text{[math]}$ 在点 $\text{[math]}$ 处的切线方程为．

答案解析收藏纠错 + 选题
16. (2022高三上·蚌埠期末) 我国无人机技术处于世界领先水平，并广泛民用于抢险救灾、视频拍摄、环保监测等领域．如图，有一个从地面A处垂直上升的无人机P，对地面B，C两受灾点的视角为 $\text{[math]}$ ，且 $\text{[math]}$ ，无人机对地面受灾点D的俯角为30°．已知地面上三处受灾点B，C，D共线，且 $\text{[math]}$ ， $\text{[math]}$ ，则无人机P到地面的距离 $\text{[math]}$ km．

答案解析收藏纠错 + 选题

三、解答题

17. (2022高三上·蚌埠期末) 已知等差数列 $\text{[math]}$ 与正项等比数列 $\text{[math]}$ 满足 $\text{[math]}$ ，且 $\text{[math]}$ ．
1. （1）求数列 $\text{[math]}$ 和数列 $\text{[math]}$ 的通项公式；
2. （2）设 $\text{[math]}$ ，求数列 $\text{[math]}$ 的前n项和 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
18. (2022高三上·蚌埠期末) 第24届冬奥会将于2022年2月4日至2月20日在北京举行，冬季两项是冬奥会的正式项目之一，冬季两项是把越野滑雪和射击两种特点不同的竞赛项目结合在一起进行的运动，要求运动员既要有由动转静的能力，又要有由静转动的能力.20km男子个人赛是冬季两项中最古老的奥运项目，分成5个阶段：第1圈滑行后卧射，第2圈滑行后立射，第3圈滑行后卧射，第4圈滑行后立射，第5圈滑行直达终点．比赛时，运动员单个出发，随身携带枪支和20发子弹，每轮射击发射5发子弹，每脱靶一次加罚1分钟．成绩的计算是越野滑雪的全程时间加被罚的时间，比赛结束所耗总时间少者获胜．已知甲、乙两名参赛选手在射击时每发子弹命中目标的概率均为0.8．
1. （1）试求甲选手在一轮射击中，被罚时间X的分布列及期望；
2. （2）若甲、乙两名选手在滑道上滑行所耗时间相同，在前三轮射击中甲选手比乙选手多罚了3分钟，试求在四轮射击结束后，甲选手所罚总时间比乙选手所罚总时间少的概率（保留小数点后4位）．
  （参考数据： $\text{[math]}$ ， $\text{[math]}$ ．）
答案解析收藏纠错 + 选题
19. (2022高三上·蚌埠期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，斜边 $\text{[math]}$ ，现将 $\text{[math]}$ 绕AC旋转一周得到一个圆锥，BD为底面圆的直径，点P为圆锥的内切球O与CD的切点， $\text{[math]}$ 为圆锥底面圆周上异于B，D的一点．
1. （1）求证： $\text{[math]}$ 平面 $\text{[math]}$ ；
2. （2）当 $\text{[math]}$ 时，求二面角 $\text{[math]}$ 的正弦值．
答案解析收藏纠错 + 选题
20. (2022高三上·蚌埠期末) “工艺折纸”是一种把纸张折成各种不同形状物品的艺术活动，在我国源远流长，某些折纸活动蕴含丰富的数学内容，例如：用一张圆形纸片，按如下步骤折纸（如下图1）
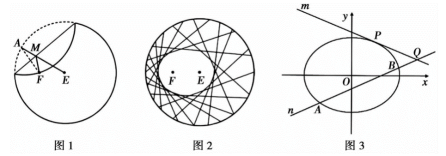
步骤1：设圆心是E，在圆内异于圆心处取一点，标记为F；
步骤2：把纸片折叠，使圆周正好通过点F；
步骤3：把纸片展开，并留下一道折痕；
步骤4：不停重复步骤2和3，就能得到越来越多的折痕（如图2）．
已知这些折痕所围成的图形是一个椭圆．若取半径为4的圆形纸片，设定点F到圆心E的距离为2，按上述方法折纸．
1. （1）以点F，E所在的直线为x轴，线段EF的中垂线为y轴，建立坐标系，求折痕所围成的椭圆C（即图1中M点的轨迹）的标准方程．
2. （2）如图3，若直线m： $\text{[math]}$ 与椭圆C相切于点P，斜率为 $\text{[math]}$ 的直线n与椭圆C分别交于点A，B（异于点P），与直线m交于点Q．证明： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 成等比数列．
答案解析收藏纠错 + 选题
21. (2022高三上·蚌埠期末) 已知函数 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ 存在极大值点．
2. （2）若函数 $\text{[math]}$ 与 $\text{[math]}$ 的图象有两个交点，求实数a的取值范围．
答案解析收藏纠错 + 选题
22. (2022高三上·蚌埠期末) 在直角坐标系xOy中，曲线C的参数方程为 $\text{[math]}$ ，其中 $\text{[math]}$ 为参数．以原点为极点，x轴的非负半轴为极轴建立极坐标系，直线l的极坐标方程为 $\text{[math]}$ ．
1. （1）求曲线C的普通方程和直线l的直角坐标方程；
2. （2）设曲线C上的点P到直线l的距离为d，求d的取值范围．
答案解析收藏纠错 + 选题
23. (2022高三上·蚌埠期末) 已知函数 $\text{[math]}$ ．
1. （1）当 $\text{[math]}$ 时，求不等式 $\text{[math]}$ 的解集；
2. （2）若 $\text{[math]}$ 成立，求实数 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题