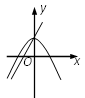
 B .
B .  C .
C . 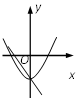 D .
D . 

解方程x4﹣7x2+12=0这是一个一元四次方程,根据该方程的特点,它的解法通常是:设x2=y,则x4=y2 , ∴原方程可化为:y2﹣7y+12=0,解得y1=3,y2=4,当y=3时,x2=3,x=± ,当y=4时,x2=4,x=±2.∴原方程有四个根是:x1=
,x2=﹣
,x3=2,x4=﹣2,以上方法叫换元法,达到了降次的目的,体现了数学的转化思想,运用上述方法解答下列问题.
①p=﹣8时,求该函数图象的顶点坐标;
②当﹣2≤x≤2时,该函数图象与x轴有且只有一个公共点,求p的取值范围;