 B .
B .  C .
C . 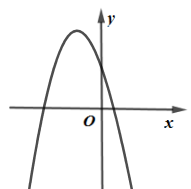 D .
D . 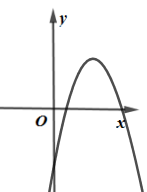
| x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
| y=ax2+bx+c | … | p | t | n | t | 0 | … |
有下列结论:①b>0;②关于x的方程ax2+bx+c=0的两个根是0和3;③p+2t<0;④m(am+b)≤﹣4a﹣c(m为任意实数).其中正确结论的个数是( )
|
x |
-3 |
-2 |
-1 |
1 |
2 |
3 |
4 |
5 |
|
y |
-14 |
-7 |
-2 |
2 |
m |
n |
-7 |
-14 |
则m-n的值为.


(1)二次函数:y=(x+1)2+2自变量x在哪个范围内,该函数单调递减?
(2)证明:函数:y=x﹣在x>1的函数范围内,该函数单调递增.
(3)若存在两个关于x的一次函数,分别记为:g=k1x+b1和h=k2x+b2 , 且函数g在实数范围内单调递增,函数h在实数范围内单调递减.记第三个一次函数y=g+h,则比例系数k1和k2满足何种条件时,函数y在实数范围内单调递增?