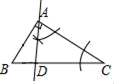
 B .
B .  C .
C .  D .
D . 
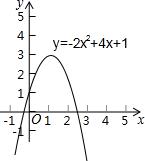

项目 | 网上学习 | 听音乐 | 聊天 | 玩游戏 | 搜索信息 |
百分比 | 92.4% | 77.1% | 73.1% | 64.7% | 55.8% |
小文发现,这些活动所占百分比之和远远超过100%,请你解释其中的原因.
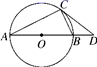
黄金分割
天文学家开普勒把黄金分割称为神圣分割,并指出,毕达哥拉斯定理(勾股定理)和黄金分割“是几何中的双宝,前者好比黄金,后者堪称珠玉”.历史上最早正式在书中使用“黄金分割”这个名称的是欧姆.19世纪以后,“黄金分割”的说法逐渐流行起来,黄金分割被广泛应用于建筑等领域.黄金分割指把一条线段分为两部分,使其中较长部分与线段总长之比等于较短部分与较长部分之比,该比值为 . 用下面的方法(如图(1))就可以作出已知线段AB的黄金分割点H;

①以线段AB为边作正方形ABCD;
②取AD的中点E,连接EB;
③延长DA到点F,使;
④以线段AF为边作正方形AFGH,点H就是线段AB的黄金分割点.
以下是证明点H就是线段AB的黄金分割点的部分过程.
证明:设正方形ABCD的边长为1,则 .
∵点E为AD的中点,∴ .
在中,
, ∴
,
∴ . ……
任务:
