 B .
B .  C .
C .  D .
D . 

 B .
B . 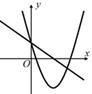 C .
C . 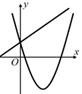 D .
D . 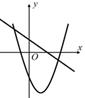
 B .
B .  C .
C .  D .
D . 

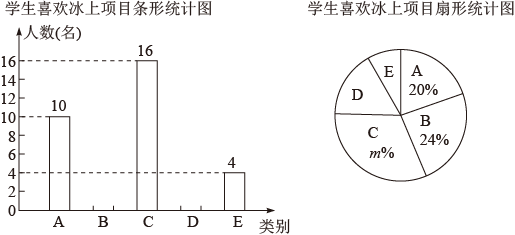
根据统计图提供的信息,解答下列问题:
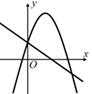
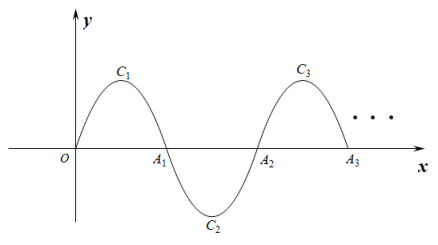
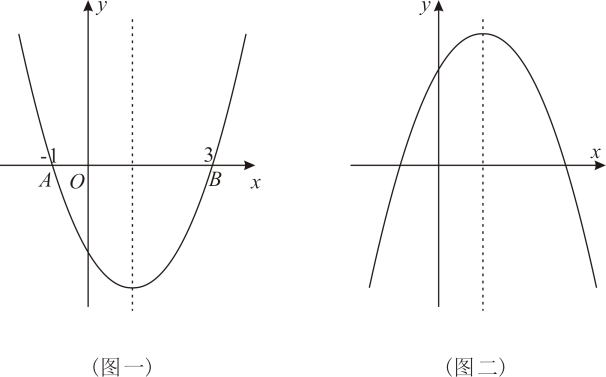
我们学习过二次函数与一元二次方程之间的关系,可以借助二次函数的图象,研究一元二次方程的根.那么我们能否借助二次函数的图象研究一元二次不等式的解集?例如:图一:与x轴的两个交点分别是
,
. 此时
有两个不相等的实数根
,
;观察图象可以知道:在x轴上方的图象所有点纵坐标大于0,此时对应的x的取值范围是
或
;所以不等式
的解集为:
或
;类比上述所了解的内容,相信你一定能够解决如下问题:
①当点P在直线BC的下方运动时,求 的面积的最大值;
②该抛物线上是否存在点P,使得 若存在,求出所有点P的坐标;若不存在,请说明理由.