广东省深圳市罗湖区翠园东晓中学2022-2023学年八年级上...

更新时间：2022-11-16 浏览次数：97 类型：期中考试

一、选择题(每题3分，共10小题，共30分每题只有一个正确选项)

1. (2022八上·罗湖期中) 下列各数是无理数的是（）

A . 0.3333 B . -2 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022八上·深圳期中) 25的平方根是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . ±5 D . 5

答案解析收藏纠错 + 选题
3. (2023八上·鄄城期中) 下列各组数中，不是勾股数的是（　　）

A . 0.3，0.4，0.5 B . 5，12，13 C . 10， 24，26 D . 7，24，25

答案解析收藏纠错 + 选题
4. (2022八上·深圳期中) 若点P的坐标为(-2022，2023)，则点P在（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
5. (2022八上·罗湖期中) 如果P (m+3，2m+4)在y轴上，那么点P的坐标是（）

A . (0，1) B . (1，0) C . (0，-2) D . (-2，0)

答案解析收藏纠错 + 选题
6. (2022八上·罗湖期中) 若m= $\text{[math]}$ -2，则估计m的值所在范围是（）

A . 1<m<2 B . 2<m<3 C . 3<m<4 D . 4<m<5

答案解析收藏纠错 + 选题
7. (2022八上·罗湖期中) 如图所示图象中，表示y是x的函数的有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
8. (2024八下·乌鲁木齐期中) 如图，将长方形纸片ABCD折叠，使边DC落在对角线AC上，折痕为CE，且D点落在对角线D'处，若AB=3，AD=4，则ED的长为（）

A . $\text{[math]}$ B . 3 C . 1 D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2022八上·罗湖期中) 如图，由四个边长为1的小正方形构成一个大正方形，连接小正方形的三个顶点，可以得到△ABC，则△ABC中AC边上的高是（）

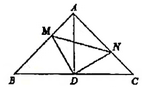
A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2022八上·罗湖期中) 如图，在△ABC中，∠BAC=90°，AB=AC=4，若点D为BC的中点，过点D作∠MDN=90°，分别交AB，AC于点M，N，连接AD，则下的出论中：①△DMN是等腰直角三角形；②△DMN的周长有最小值；③四边形AMDN的面积为定值8；④△DMN的面积有最小值。正确的有（）

A . 4个 B . 3个 C . 2个 D . 1个

答案解析收藏纠错 + 选题

二、填空题(本大题共5小題，每小题3分，共15分)

11. (2024七上·龙湾期中) 8的立方根是．

答案解析收藏纠错 + 选题
12. (2022八上·罗湖期中) 点A (-4，3)关于x轴的对称点的坐标是

答案解析收藏纠错 + 选题
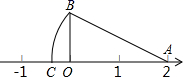
13. (2022八上·罗湖期中) 如图数轴上的点O表示的数是0，点A表示的数是2， $\text{[math]}$ ，垂足为O，且 $\text{[math]}$ ，以A为圆心， $\text{[math]}$ 长为半径画弧，交数轴于点C，则点C表示的数为.

答案解析收藏纠错 + 选题
14. (2023八上·广州期中) 从甲地向乙地打长途电话，按时间收费，3分钟内收费2.4元，每加1分钟加收1元，若时间t≥3(分)时，电话费y(元)与t(分)之间的函数关系式是．

答案解析收藏纠错 + 选题
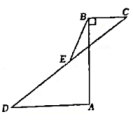
15. (2022八上·罗湖期中) 如图，AB⊥BC于点B，AB⊥AD于点小，点E是CD中点，若BC=5，AD=12，BE=12.5，则AB的长是

答案解析收藏纠错 + 选题

三、解答题(本大题共7小题，其中第16题12分，第17题5分，第18题6分，第19题6分，第20题7分，第21题9分，第22题10分，共55分)

16. (2022八上·罗湖期中) 计算：
1. （1） |-2|+(3- $\text{[math]}$ )⁰+ $\text{[math]}$
2. （2） $\text{[math]}$
3. （3） $\text{[math]}$
4. （4） $\text{[math]}$
答案解析收藏纠错 + 选题
17. (2022八上·罗湖期中) 如图，甲船以16海里/时的速度离开港口，向东南航行，乙船在同时同地向西南方向航行，已知他们离开港口一个半小时后分别到达B、A两点，月知AB=30海里，问乙船每小时航行多少海里？

答案解析收藏纠错 + 选题
18. (2022八上·罗湖期中)
( 1 )作出△ABC关于y独对称的图形△A₁B₁C₁：
( 2 )直接写出点C关于x铀对称C₂的坐标：；
( 3 )在y轴上找一点P，使得△PAC周长最小。请在图中标出点P的位置．

答案解析收藏纠错 + 选题
19. (2022八上·罗湖期中) 将长为38cm，宽为5cm的长万形白纸拔如图所示的方法黏合在一起，黏合部分的白纸宽为2cm．
1. （1）求5张白纸黏合的长度：
2. （2）设x张白纸黏合后的总长为ycm，写出y与x的函数关系式
答案解析收藏纠错 + 选题
20. (2022八上·罗湖期中) 如图，△ACB和△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，D为AB边上一点。
1. （1）求证：△ACE≌△BCD：
2. （2）若CB= $\text{[math]}$ ， AD=2，求DE的长．
答案解析收藏纠错 + 选题
21. (2022八上·罗湖期中) 如图所示，四边形ABCD，∠A=90°，AB=3m，BC=12m，CD=13m，DA=4m，
1. （1）求证：BD⊥CB
2. （2）求四边形ABCD的面积．
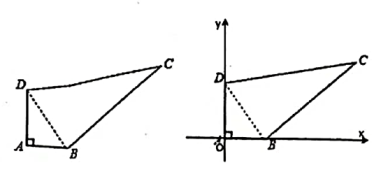
3. （3）如图，以A为坐标原点，以AB、AD所在直线为x轴、y轴建立直角坐标系，点P在y轴上，若S_△P_BD= $\text{[math]}$ S_{四边形ABCD} ，求P的坐标。
答案解析收藏纠错 + 选题
22. (2022八上·罗湖期中) 如图，已知△ABC中，∠B=90°，AB=8cm，BC=6cm，P、Q是△ABC边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B开始沿B→C→A方向运动，且速度为每秒2cm，它们同时出发，设出发的时间为1秒．
1. （1）出发2秒后，求PQ的长；
2. （2）当点Q在边BC上运动时，出发几秒钟，APQB能形成等腰三角形？
3. （3）当点Q在边CA上运动时，求能使ABCQ成为等腰三角形的运动时间(直接写出答案)．
答案解析收藏纠错 + 选题