四川省成都市简阳市2021-2022学年八年级上学期期末数学...

更新时间：2022-12-29 浏览次数：64 类型：期末考试

一、单选题

1. (2021八下·辛集期末) 下列实数中的无理数是（）

A . 0 B . $\text{[math]}$ C . $\text{[math]}$ D . 1.01010101…

答案解析收藏纠错 + 选题
2. (2021九上·甘井子期中) 若点P（2，﹣3），则点P关于原点的对称点的坐标是（）

A . （2，3） B . （﹣2，﹣3） C . （﹣2，3） D . （2，﹣3）

答案解析收藏纠错 + 选题
3. (2021八上·成都期末) 下列给出的四组数中，能构成直角三角形三边的一组是（）

A . 3，4，5 B . 5，12，14 C . 6，8，9 D . 8，13，15

答案解析收藏纠错 + 选题
4. (2020·泰州) 下列等式成立的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2021八上·成都期末) 下列命题是真命题的是（）

A . 如果两个角是内错角，那么它们一定相等 B . 如果两个角是同位角，那么它们一定相等 C . 如果两个角是同旁内角，那么它们一定互补 D . 如果两个角是对顶角，那么它们一定相等

答案解析收藏纠错 + 选题
6. 一次函数y＝7x-6的图象不经过（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
7. (2021八上·成都期末) 已知点（﹣2，y₁），（3，y₂）都在直线y＝﹣x﹣5上，则y₁ ， y₂的值的大小关系是（）

A . y₁＜y₂ B . y₁＞y₂ C . y₁＝y₂ D . 不能确定

答案解析收藏纠错 + 选题

8. (2021八上·成都期末) 下表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差：

	甲	乙	丙	丁
平均数（环）	9.5	9.5	9.5	9.5
方差	8.5	7.3	8.8	7.7

根据表中数据，要从中选择一名成绩发挥稳定的运动员参加比赛，应选择（）

A . 甲 B . 乙 C . 丙 D . 丁

答案解析收藏纠错 + 选题

9. (2021八上·武侯期末) 如图，一次函数y＝2x和y＝ax+4的图象相交于点A（m，3），则关于x，y的方程组 $\text{[math]}$ 的解为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

10. (2021八上·成华期末) 实数2﹣ $\text{[math]}$ 的倒数是.

答案解析收藏纠错 + 选题
11. 已知一次函数的图象经过点 $\text{[math]}$ ，且与直线 $\text{[math]}$ 平行，则一次函数的表达式为.

答案解析收藏纠错 + 选题
12. (2021八上·成都期末) 《九章算术》是我国古代一部著名的算书，它的出现标志着中国古代数学形成了完整的体系其中卷八方程[七]中记载：“今有牛五、羊二，直金十两.牛二、羊五，直金八两.牛、羊各直金几何？”题目大意是：5头牛、2只羊共值金10两.2头牛、5只羊共值金8两.每头牛、每只羊各值金多少两？设1头牛值金 $\text{[math]}$ 两，1只羊值金 $\text{[math]}$ 两，则可列方程组为.

答案解析收藏纠错 + 选题
13. (2022八下·临清期中) 如图，正方形ABCD的边长为1，其面积标记为S₁ ，以AB为斜边向外作等腰直角三角形，再以该等腰直角三角形的一条直角边为边向外作正方形，其面积标记为S₂ ， …按照此规律继续下去，则S₇的值为．

答案解析收藏纠错 + 选题
14. 若 $\text{[math]}$ +（y-1）²＝0，则（x+y）²⁰²¹等于.

答案解析收藏纠错 + 选题
15. 若关于x，y的二元一次方程组 $\text{[math]}$ 的解也是二元一次方程x+0.6y=36的解，则k的值为.

答案解析收藏纠错 + 选题
16. 若一个直角三角形的三边长分别为x，12，13，则x=.

答案解析收藏纠错 + 选题
17. 如图，△ABC是等腰直角三角形，AC=BC，∠ACB=90°，点D是AB中点，在△ABC外取一点E，使DE=AD，连接DE，AE，BE，CE.若CE= $\text{[math]}$ - $\text{[math]}$ ， ∠ABE=30°，则AE的长为 .

答案解析收藏纠错 + 选题
18. 正方形A₁B₁C₁O，A₂B₂C₂C₁ ， A₃BC₃C₂ ， …按如图所示的方式放置.点A₁ ， A₂ ， A₃ ， …和点C₁ ， C₂ ， C₃ ， …分别在直线y＝kx+b（k＞0）和y轴上，已知点B₁（1，1），B₂（2，3），则点B₃的坐标是，点Bn的坐标是 .

答案解析收藏纠错 + 选题

三、解答题

19. (2021八上·成都期末) 计算.
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
20. 解方程：
1. （1）解方程组： $\text{[math]}$ ；
2. （2）解方程组： $\text{[math]}$ .
答案解析收藏纠错 + 选题
21. (2021八上·双流月考) 已知 $\text{[math]}$ ABC的三个顶点坐标分别为A(﹣1，4)，B(﹣3，4)，C(﹣5，2).
1. （1）请在坐标平面内画出 $\text{[math]}$ ABC；
2. （2）请在y轴上找一点P，使线段AP与BP的和最小，并直接写出P点坐标（保留作图痕迹）.
答案解析收藏纠错 + 选题
22. (2021八上·成都期末) 为了解学生每天回家完成作业时间情况，某中学对学生每天回家完成作业时间进行抽样调查，并将调查结果绘制成如图两幅不完整的统计图，根据图示，请回答下列问题：
1. （1）被抽样调查的学生有 ▲ 人，并补全条形统计图；
2. （2）每天回家完成作业时间的中位数是（小时），众数是（小时）；
3. （3）该校共有2000名学生，请估计该校每天回家完成作业时间超过2小时的学生有多少人？
答案解析收藏纠错 + 选题
23. 如图，已知直线l₁经过点A（5，0），B（1，4），与直线l₂：y＝2x-4交于点C，且直线1₂交x轴于点D.
1. （1）求直线l₁的函数表达式；
2. （2）求直线l₁与直线l₂交点C的坐标；
3. （3）求 $\text{[math]}$ ADC的面积.
答案解析收藏纠错 + 选题
24. 已知，△ABC和△DCE都是等边三角形，点B，C，E三点不在一条直线上（如图1）.
1. （1）求证：BD＝AE；
2. （2）若∠ADC=30°，AD=4，CD=5，求BD的长；
3. （3）若点B，C，E三点在一条直线上（如图2），且△ABC和△DCE的边长分别为3和5，求AD的长.
答案解析收藏纠错 + 选题
25. 某校准备组织八年级280名学生和5名老师参加研学活动，已知用1辆小客车和2辆大客车每次可运送120人；用3辆小客车和1辆大客车每次可运送135人.
1. （1）每辆小客车和每辆大客车各能坐多少人？
2. （2）若学校计划租用小客车m辆，大客车n辆，一次送完，且恰好每辆车都坐满.
  ①请你设计出所有的租车方案；
  
  ②若小客车每辆需租金6000元，大客车每辆需租金7500元，总租金为W元，写出W与m的关系式，根据关系式选出最省钱的租车方案，并求出最少租金.
答案解析收藏纠错 + 选题
26. 如图1，在△ABC中，AB=AC，∠BAC=90°，D为AC边上一动点，且不与点A、点C重合，连接BD并延长，在BD延长线上取一点E，使AE=AB，连接CE.
1. （1）若∠AED＝20°，则∠DEC＝度；
2. （2）若∠AED＝α，试探索∠AED与∠AEC有怎样的数量关系？并证明你的猜想；
3. （3）如图2，延长EC到点H，连接BH²+CH²＝2AE² ，连接AH与BE交于F，试探究BE与FH的关系.
答案解析收藏纠错 + 选题
27. 如图，已知直线y=x-2分别与x轴，y轴交于A，B两点，直线OG：y=kx（k＜0）交AB于点D.
1. （1）求A，B两点的坐标；
2. （2）如图1，点E是线段OB的中点，连接AE，点F是射线OG上一点，当OG⊥AE，且OF=AE时，
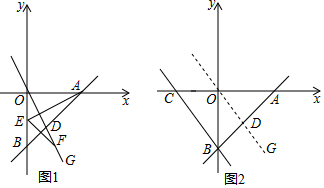
  ①求EF的长；
  
  ②在x轴上找一点P，使PE+PD的值最小，求出P点坐标.
3. （3）如图2，若k＝- $\text{[math]}$ ，过B点BC∥OG，交x轴于点C，此时在坐标平面内是否存在点M，使△BCM是以BC为腰的等腰直角三角形，若存在，直接写出点M的坐标；若不存在，请说明理由
答案解析收藏纠错 + 选题