山东省德州市庆云县2022-2023学年九年级上学期期中数学...

更新时间：2023-01-31 浏览次数：69 类型：期中考试

一、单选题

1. (2022九上·庆云期中) 下列美丽的图案，是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2022九上·庆云期中) 若关于x的方程（m﹣1）x²+mx﹣1＝0是一元二次方程，则m的取值范围是（）

A . m≠1 B . m＝1 C . m≥1 D . m≠0

答案解析收藏纠错 + 选题
3. (2022九上·庆云期中) 如图，AB为⊙O的弦，直径CD⊥AB，交AB于点H，连接OA，若∠A＝45°，AB＝2，则DH的长度为（　　）

A . 1 B . $\text{[math]}$ ＋1 C . 2 $\text{[math]}$ －1 D . 3

答案解析收藏纠错 + 选题
4. (2022九上·合江期末) 将二次函数 $\text{[math]}$ 的图象向右平移2个单位，再向上平移3个单位得到该二次函数的表达式是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024九上·芙蓉开学考) 设方程x²+x﹣2=0的两个根为α，β，那么（α﹣2）（β﹣2）的值等于（　　）

A . ﹣4 B . 0 C . 4 D . 2

答案解析收藏纠错 + 选题
6. (2022九上·庆云期中) 如图，将一个含30°角的直角三角板 $\text{[math]}$ 绕点A旋转，使得点B，A， $\text{[math]}$ 在同一条直线上，则旋转角的度数是（）

A . 30° B . 60° C . 120° D . 150°

答案解析收藏纠错 + 选题
7. (2023九上·遵义月考) 若关于x的一元二次方程kx²-2x-1＝0有两个实数根，则k的取值范围是（　　）

A . k≠0 B . k≥-1 C . k≥-1且k≠0 D . k＞-1且k≠0

答案解析收藏纠错 + 选题
8. (2024九上·深圳开学考) 如图，将 $\text{[math]}$ 绕点A按顺时针旋转一定角度得到 $\text{[math]}$ ，点B的对应点D恰好落在BC边上，若 $\text{[math]}$ ，则CD的长为（）

A . 1 B . $\text{[math]}$ C . 2 D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2022九上·庆云期中) 二次函数 $\text{[math]}$ 的图象如图所示，若 $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 在该函数的图象上，则 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 的大小关系是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2022九上·庆云期中) 下列说法中，正确的个数为（　　）
⑴在同圆或等圆中，弦相等则所对的弧相等；
⑵优弧一定比劣弧长；
⑶弧相等则所对的圆心角相等；
⑷在同圆或等圆中，圆心角相等则所对的弦相等．

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
11. (2022九上·庆云期中) 在某圆形喷水池的池中心竖直安装一根水管，在水管的顶端安一个喷水头，以水管与地面交点为原点，原点与水柱落地处所在直线为x轴，建立如图所示的平面直角坐标系，若喷出的抛物线形水柱解析式为 $\text{[math]}$ （0≤x≤3），则水管长为（）

A . 1m B . 2m C . $\text{[math]}$ m D . 3m

答案解析收藏纠错 + 选题
12. (2022九上·庆云期中) 如图，点A、B分别在x轴、y轴上（ $\text{[math]}$ ）；以 $\text{[math]}$ 为直径的圆经过原点O，C是 $\text{[math]}$ 的中点，连结 $\text{[math]}$ ， $\text{[math]}$ ．下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的面积等于5；④若 $\text{[math]}$ ，则点C的坐标是 $\text{[math]}$ ，其中正确的结论有（　　）

A . 4个 B . 3个 C . 2个 D . 1个

答案解析收藏纠错 + 选题

二、填空题

13. (2024九上·江海期末) $\text{[math]}$ 是关于x的一元二次方程 $\text{[math]}$ 的解，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
14. (2023九上·金平月考) 若点A(4，n)与点B(－m，6)关于原点对称，则m＋n＝．

答案解析收藏纠错 + 选题
15. (2022九上·庆云期中) 给出一种运算：对于函数 $\text{[math]}$ ，规定 $\text{[math]}$ ．例如：若函数 $\text{[math]}$ ，则有 $\text{[math]}$ ．若函数 $\text{[math]}$ ，求方程 $\text{[math]}$ 的解为．

答案解析收藏纠错 + 选题
16. (2022九上·庆云期中) 已知：二次函数y=ax²+bx+c图像上部分点的横坐标x与纵坐标y的对应值如表格所示，那么它的图像与x轴的另一个交点坐标是．
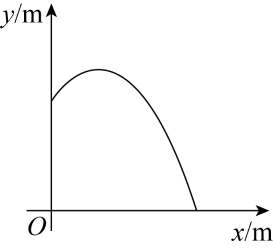
x
…
-1
0
1
2
…
y
…
0
3
4
3
…

答案解析收藏纠错 + 选题
17. (2022九上·庆云期中) 如图，在 $\text{[math]}$ 中，弦 $\text{[math]}$ ，点C在 $\text{[math]}$ 上移动，连结 $\text{[math]}$ ，过点C作 $\text{[math]}$ 交 $\text{[math]}$ 于点D，则 $\text{[math]}$ 的最大值为．

答案解析收藏纠错 + 选题
18. (2022九上·庆云期中) 在平面直角坐标系中，将如图所示的 $\text{[math]}$ 按照如下图所示的方式依次进行轴对称变换，若点A坐标是 $\text{[math]}$ ，则经过第2022次变换后所得的点 $\text{[math]}$ 坐标是．

答案解析收藏纠错 + 选题

三、解答题

19. (2022九上·庆云期中) 解方程：
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
20. (2022九上·庆云期中) 抛物线 $\text{[math]}$ 与x轴交于A、B两点（A在B的右侧），与y轴交于点C．
1. （1）求线段 $\text{[math]}$ 的长；
2. （2）判断 $\text{[math]}$ 的形状．
答案解析收藏纠错 + 选题
21. (2022九上·庆云期中) 如图，平面直角坐标系内，小正方形网格的边长为1个单位长度，△ABC的三个顶点的坐标分别为A（-1，3），B（-4，0），C．（0，0）
（ 1 ）将△ABC向上平移1个单位长度，再向右平移5个单位长度后得到的△A₁B₁C₁ ，画出△A₁B₁C₁ ，并直接写出点A₁的坐标；
（ 2 ）△ABC绕原点O逆时针方向旋转90°得到△A₂B₂O；
（ 3 ）如果△A₂B₂O，通过旋转可以得到△A₁B₁C₁ ，请直接写出旋转中心P的坐标

答案解析收藏纠错 + 选题
22. (2022九上·庆云期中) 如图，某小区矩形绿地的长、宽分别为35m和15m，现计划对其进行扩充，将绿地的长宽增加相同的长度后，得到一个新的矩形绿地．
1. （1）若扩充后的矩形绿地面积为 $\text{[math]}$ ，求新的矩形绿地长与宽．
2. （2）若扩充后，实地测量发现新的矩形绿地的长宽之比为5：3，求新的矩形绿地面积．
答案解析收藏纠错 + 选题
23. (2022九上·庆云期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，以 $\text{[math]}$ 为直径作 $\text{[math]}$ ，交 $\text{[math]}$ 边于点D，在 $\text{[math]}$ 上取一点E，使 $\text{[math]}$ ，连接 $\text{[math]}$ ，作射线 $\text{[math]}$ 交 $\text{[math]}$ 边于点F．
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
24. (2023八上·凤凰期末) 阅读下列材料：
利用完全平方公式，可以将多项式 $\text{[math]}$ 变形为 $\text{[math]}$ 的形式，我们把这样的变形方法叫做多项式 $\text{[math]}$ 的配方法．运用多项式的配方法及平方差公式能对一些多项式进行分解因式．

例如： $\text{[math]}$

＝ $\text{[math]}$

＝ $\text{[math]}$

＝ $\text{[math]}$

＝ $\text{[math]}$

根据以上材料，解答下列问题：
1. （1）用多项式的配方法将 $\text{[math]}$ 化成 $\text{[math]}$ 的形式；
2. （2）下面是某位同学用配方法及平方差公式把多项式 $\text{[math]}$ 进行分解因式的解答过程：
  
  老师说，这位同学的解答过程中有错误，请你找出该同学解答中开始出现错误的地方，并用“ ”标画出来，然后写出完整的、正确的解答过程：
3. （3）求证：x，y取任何实数时，多项式 $\text{[math]}$ 的值总为正数．
答案解析收藏纠错 + 选题
25. (2023·即墨模拟) 如图，题目中的黑色部分是被墨水污染了无法辨认的文字，导致题目缺少了一个条件而无法解答，经查询结果发现，该二次函数解析式 $\text{[math]}$ ，

已知二次函数 $\text{[math]}$ 的图象经过点 $\text{[math]}$ ， $\text{[math]}$ ，．

求该二次函数的解析式．
1. （1）请根据已有信息添加一个适当的条件：
2. （2）当函数值 $\text{[math]}$ ，自变量x的取值范围为：
3. （3）如图1，将函数 $\text{[math]}$ 的图象向右平移4个单位与 $\text{[math]}$ 的图象组成一个新的函数图象，记为L，若点 $\text{[math]}$ ，求m的值．
4. （4）如图2，在（3）的条件下，点A的坐标为 $\text{[math]}$ ，在L上是否存在点Q，使得 $\text{[math]}$ ，若存在，求出所有满足条件的点Q的坐标，不存在，说明理由．
答案解析收藏纠错 + 选题