山东省青岛市即墨区2023年中考一模数学试题

更新时间：2024-07-13 浏览次数：119 类型：中考模拟

一、单选题

1. (2024·广水模拟) $\text{[math]}$ 的相反数是（）

A . 2 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023九上·武昌期中) 2022年4月16日，神舟十三号载人飞船圆满完成全部既定任务，顺利返回地球家园．六个月的飞天之旅展现了中国航天科技的新高度下列航天图标，其文字上方的图案是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2023·即墨模拟) 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023·佛山模拟) 如图， $\text{[math]}$ 内接于 $\text{[math]}$ ， AD是 $\text{[math]}$ 的直径，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数是（）

A . 60° B . 65° C . 70° D . 75°

答案解析收藏纠错 + 选题
5. (2023九上·盐山月考) 若关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 有两个不相等的实数根，且k为非负整数，则符合条件的k的个数为（）

A . 0个 B . 1个 C . 2个 D . 3个

答案解析收藏纠错 + 选题
6. (2023·即墨模拟) 如图，正方形 $\text{[math]}$ 的边长为 $\text{[math]}$ ，将正方形 $\text{[math]}$ 绕原点O顺时针旋转45°，则点B的对应点 $\text{[math]}$ 的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024·威远模拟) 如图，在边长为4的菱形ABCD中，E为AD边的中点，连接CE交对角线BD于点F．若∠DEF＝∠DFE，则这个菱形的面积为（）

A . 16 B . 6 $\text{[math]}$ C . 12 $\text{[math]}$ D . 30

答案解析收藏纠错 + 选题
8. (2023·即墨模拟) 平面直角坐标系中，二次函数 $\text{[math]}$ 的图象如图所示，现给出下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ （m为实数）；⑤ $\text{[math]}$ ．其中正确结论的个数是（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题

二、填空题

9. (2023·即墨模拟) 粮食是人类赖以生存的重要物质基础.2022年我国粮食总产量再创新高，达 $\text{[math]}$ 万吨．比2021年增加368吨，增长 $\text{[math]}$ ， $\text{[math]}$ 万可用科学记数法表示为．

答案解析收藏纠错 + 选题
10. (2023·即墨模拟) 计算， $\text{[math]}$ ．

答案解析收藏纠错 + 选题
11. (2023·即墨模拟) 若一组数据 $\text{[math]}$ 的平均数为6，众数为5，则这组数据的方差为．

答案解析收藏纠错 + 选题
12. (2023·即墨模拟) 某品牌瓶装饮料每箱价格是26元，某商店对该瓶装饮料进行“买一送三”的促销活动，即整箱购买，则买一箱送三瓶，这相当于每瓶比原价便宜了0.6元，问该品牌饮料每瓶多少元？设该品牌饮料每瓶是x元，则可列方程为．

答案解析收藏纠错 + 选题
13. (2023·即墨模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，以 $\text{[math]}$ 为直径的 $\text{[math]}$ 交 $\text{[math]}$ 于点D，弧 $\text{[math]}$ 沿直线 $\text{[math]}$ 翻折后经过点O，那么阴影部分的面积为．

答案解析收藏纠错 + 选题
14. (2023·即墨模拟) 如图，在正方形ABCD中，点E是边BC上的一点，点F在边CD的延长线上，且 $\text{[math]}$ ，连接EF交边AD于点G．过点A作 $\text{[math]}$ ，垂足为点M，交边CD于点N．若 $\text{[math]}$ ， $\text{[math]}$ ，则线段AN的长为

答案解析收藏纠错 + 选题

三、解答题

15. (2023·即墨模拟) 已知：在 $\text{[math]}$ 及 $\text{[math]}$ 边上一点E．求作： $\text{[math]}$ ，使它分别于 $\text{[math]}$ 相切，且点E为其中一个切点．

答案解析收藏纠错 + 选题
16. (2023·即墨模拟)
1. （1）化简： $\text{[math]}$
2. （2）解方程组 $\text{[math]}$
答案解析收藏纠错 + 选题
17. (2023·即墨模拟) 有四张背面相同的纸牌A，B，C，D，其正面分别画有四个不同的几何图形（如图）.小华将这4张纸牌背面朝上洗匀后摸出一张，放回洗匀后再摸出一张.
1. （1）用树状图（或列表法）表示两次模牌所有可能出现的结果（纸牌可用A、B、C、D表示）；
2. （2）求摸出两张牌面图形都是中心对称图形的纸牌的概率.
答案解析收藏纠错 + 选题
18. (2023·即墨模拟) 已知二次函数 $\text{[math]}$
1. （1）求证：二次函数 $\text{[math]}$ 的图像与x轴总有两个交点
2. （2）若二次函数 $\text{[math]}$ 的图像与x轴交点的横坐标一个大于2，一个小于1，求m的取值范围．
答案解析收藏纠错 + 选题
19. (2024·阳新) 为落实“双减”政策，优化作业管理，某中学从全体学生中随机抽取部分学生，调查他们每天完成书面作业的时间t（单位：分钟）.按照完成时间分成五组：A组“t≤45”，B组“45＜t≤60”，C组“60＜t≤75”，D组“75＜t≤90”，E组“t＞90”.将收集的数据整理后，绘制成如下两幅不完整的统计图. 根据以上信息，解答下列问题：
1. （1）这次调查的样本容量是 ▲ ，请补全条形统计图；
2. （2）在扇形统计图中，B组的圆心角是度，本次调查数据的中位数落在组内；
3. （3）若该校有1800名学生，请你估计该校每天完成书面作业不超过90分钟的学生人数.
答案解析收藏纠错 + 选题
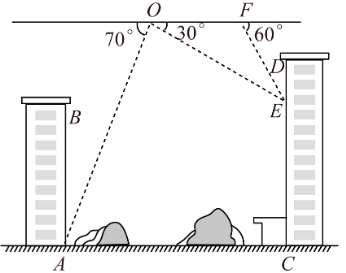
20. (2023·即墨模拟) 随着科技的发展，无人机已广泛应用于生产和生活，如代替人们在高空测量距离和角度.某校“综合与实践”活动小组的同学要测星AB，CD两座楼之间的距离，他们借助无人机设计了如下测量方案：无人机在AB，CD两楼之间上方的点O处，点O距地面AC的高度为60m，此时观测到楼AB底部点A处的俯角为70°，楼CD上点E处的俯角为30°，沿水平方向由点O飞行24m到达点F，测得点E处俯角为60°，其中点A，B，C，D，E，F，O均在同一竖直平面内.请根据以上数据求楼AB与CD之间的距离AC的长（结果精确到1m.参考数据： $\text{[math]}$ ）.

答案解析收藏纠错 + 选题
21. (2023·即墨模拟) 如图1，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点D，E分别是边 $\text{[math]}$ ， $\text{[math]}$ 的中点，连接 $\text{[math]}$ ．将 $\text{[math]}$ 绕点C逆时针方向旋转，记旋转角为 $\text{[math]}$ ．
1. （1）问题发现
  ①当 $\text{[math]}$ 时， $\text{[math]}$ ；
  ②当 $\text{[math]}$ 时， $\text{[math]}$ ；
2. （2）拓展探究：试判断当 $\text{[math]}$ 时， $\text{[math]}$ 的大小有无变化？请仅就图2的情形给出证明；
答案解析收藏纠错 + 选题
22. (2023·即墨模拟) 如图，直线 $\text{[math]}$ ， $\text{[math]}$ 都与双曲线 $\text{[math]}$ 交于点 $\text{[math]}$ ，这两条直线分别与x轴交于B，C两点．
1. （1）求y与x之间的函数关系式；
2. （2）直接写出当 $\text{[math]}$ 时，不等式 $\text{[math]}$ 的解集；
3. （3）若点P在x轴上，连接 $\text{[math]}$ 把 $\text{[math]}$ 的面积分成 $\text{[math]}$ 两部分，求此时点P的坐标．
答案解析收藏纠错 + 选题
23. (2023·即墨模拟) 在菱形 $\text{[math]}$ 中， $\text{[math]}$ 分别是其外角 $\text{[math]}$ 和 $\text{[math]}$ 的平分线， $\text{[math]}$ 的延长线交 $\text{[math]}$ 于点E， $\text{[math]}$ 的延长线交 $\text{[math]}$ 于点F．
1. （1）证明： $\text{[math]}$
2. （2）判断四边形 $\text{[math]}$ 是什么特殊四边形．并说明理由．
答案解析收藏纠错 + 选题
24. (2024九上·市南区期末) 跳绳项目在中考体考中易得分，是大多数学生首选的项目，在中考体考来临前，某文具店看准商机购进甲、乙两种跳绳．已知甲、乙两种跳绳进价单价之和为32元；甲种跳绳每根获利4元，乙种跳绳每根获利5元；店主第一批购买甲种跳绳25根、乙种跳绳30根一共花费885元．
1. （1）甲、乙两种跳绳的单价分别是多少元？
2. （2）若该文具店预备第二批购进甲、乙两种跳绳共60根，在费用不超过1000元的情况下，如何进货才能保证利润W最大？
3. （3）由于质量上乘，前两批跳绳很快售完，店主第三批购进甲、乙两种跳绳若干，当甲、乙两种跳绳保持原有利润时，甲、乙两种跳绳每天分别可以卖出120根和105根，后来店主决定将甲、乙两种跳绳的售价同时提高相同的售价，已知甲、乙两种跳绳每提高1元均少卖出5根，为了每天获取更多利润，请问店主将两种跳绳同时提高多少元时，才能使日销售利润达到最大？
答案解析收藏纠错 + 选题
25. (2023·即墨模拟) 如图，题目中的黑色部分是被墨水污染了无法辨认的文字，导致题目缺少了一个条件而无法解答，经查询结果发现，该二次函数解析式 $\text{[math]}$ ，

已知二次函数 $\text{[math]}$ 的图象经过点 $\text{[math]}$ ， $\text{[math]}$ ，．

求该二次函数的解析式．
1. （1）请根据已有信息添加一个适当的条件：
2. （2）当函数值 $\text{[math]}$ ，自变量x的取值范围为：
3. （3）如图1，将函数 $\text{[math]}$ 的图象向右平移4个单位与 $\text{[math]}$ 的图象组成一个新的函数图象，记为L，若点 $\text{[math]}$ ，求m的值．
4. （4）如图2，在（3）的条件下，点A的坐标为 $\text{[math]}$ ，在L上是否存在点Q，使得 $\text{[math]}$ ，若存在，求出所有满足条件的点Q的坐标，不存在，说明理由．
答案解析收藏纠错 + 选题