广西南宁市第十三中学2022-2023学年九年级上学期第三次...

更新时间：2024-07-29 浏览次数：72 类型：月考试卷

一、选择题（共36分）

1. (2022九上·南宁月考) 下列图形是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2022九上·南宁月考) 2020年国庆中秋假日期间，广西共接待游客超32550000人次，按可比口径同比恢复85.6%，实现旅游消费接近224亿元，按可比口径同比恢复85.9%.数据32550000用科学记数法表示为（）

A . 3255×10⁴ B . 3.255×10⁷ C . 3.255×10⁴ D . 32.55×10⁶

答案解析收藏纠错 + 选题
3. (2022九上·南宁月考) 如图点O为数轴的原点，若点A表示的数是a，点B表示的数是b，那么下列关系正确的是（）

A . a＞0 B . b＜0 C . a＜b D . a＞b

答案解析收藏纠错 + 选题
4. (2022九上·南宁月考) 某高中饭堂为了了解学生对四种早餐套餐的喜爱程度，随机抽取在校200名学生进行最爱最喜爱早餐套餐的调查（每人选一种），绘制了如图的扇形统计图.根据图中的信息，学生最喜欢的套餐种类是（）

A . 套餐A B . 套餐B C . 套餐C D . 套餐D

答案解析收藏纠错 + 选题
5. (2022九上·南宁月考) 下列计算正确的是（）

A . 3x²+2x²＝5x⁴ B . x³•x³＝2x³ C . （x⁴）³＝x⁷ D . 10ab³÷（-5ab）＝-2b²

答案解析收藏纠错 + 选题
6. (2022九上·南宁月考) 如图，AB∥EF，∠ABC＝80°，∠CDF＝135°，则∠BCD的度数为（）

A . 30° B . 35° C . 55° D . 80°

答案解析收藏纠错 + 选题
7. (2022九上·南宁月考) “漏壶”是古代一种计时器，在它内部盛一定量的水，不考虑水量变化对压力的影响，水从壶底小孔均匀漏出，壶内壁有刻度.人们根据壶中水面的位置计算时间.在漏壶漏完水之前，漏壶内水的深度与对应的漏水时间满足的函数关系式（）

A . 正比例函数关系 B . 一次函数关系 C . 反比例函数关系 D . 二次函数关系

答案解析收藏纠错 + 选题
8. (2022九上·南宁月考) 一个不透明布袋里有四个完全相同的小球，把它们分别标号为1，2，3，5，从中任意摸出一个球，记下编号后放回，搅匀，再任意摸出一个球，则两次摸出的球的编号之和为偶数的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2022九上·南宁月考) 我国古代数学名作《九章算术》中记载了“圆材埋壁”问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”其大意为：如图，现有圆柱状的木材埋在墙壁里，不知道其宽度的大小，于是用锯子（沿横截面）锯它，当量得深度CE＝1寸的时候，锯开的宽度AB＝1尺（1尺＝10寸），问木材的直径CD的长是（）

A . $\text{[math]}$ 寸 B . 10寸 C . 13寸 D . 26寸

答案解析收藏纠错 + 选题
10. (2022九上·南宁月考) 学期即将结束，某班家委为班上获得“文明学生”和“劳动积极分子”称号的学生准备A、B两种礼物.A、B两种礼物的总价分别为450元和420元，且A种礼物比B种礼物多10份，A、B两种礼物的单价分别是这一批礼物平均单价的0.9倍和1.2倍，这一批礼物平均单价是（）

A . 15元 B . $\text{[math]}$ 元 C . 10元 D . 8.5元

答案解析收藏纠错 + 选题
11. (2022九上·南宁月考) 如图是树枝的一部分，一只蚂蚁M以2cm/s的速度从树枝的A点处出发沿树枝AB方向向上爬行，另一只蚂蚁N从O点出发，以1cm/s的速度沿树枝OC方向爬行，如果AB，OC足够长，OA＝12cm，∠BOC＝60°，且两只蚂蚁同时出发，用t（s）表示爬行的时间，当两只蚂蚁与点O恰好构成等腰三角形时，t的值是（）

A . 4s B . 12s C . 4s或12s D . 4s或12s或16s

答案解析收藏纠错 + 选题
12. (2022九上·南宁月考) 如图，已知点 $\text{[math]}$ .点P是反比例函数 $\text{[math]}$ 图象上一动点，已知点P到点 $\text{[math]}$ 的距离等于点P到直线AB距离的 $\text{[math]}$ 倍，PM∥x轴交直线AB于点M，则PM+PN的最小值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（共18分.）

13. (2024九下·凉州模拟) 计算：|﹣ $\text{[math]}$ |=．

答案解析收藏纠错 + 选题
14. (2022九上·南宁月考) 分式 $\text{[math]}$ 的值为0，则x的值是 .

答案解析收藏纠错 + 选题
15. (2022九上·南宁月考) 已知 $\text{[math]}$ 的结果为正整数，则正整数n的最小值为.

答案解析收藏纠错 + 选题
16. (2022九上·南宁月考) 如图，△ABC≌△DEC，若∠D＝30°，且CD∥AB，则∠B的度数是 °.

答案解析收藏纠错 + 选题
17. (2022九上·南宁月考) 不等式组 $\text{[math]}$ 的解集是 .

答案解析收藏纠错 + 选题
18. (2022九上·南宁月考) 如图，在矩形ABCD中，AB＝6，BC＝4，以A为圆心，AD长为半径画弧交AB于点E，以C为圆心，CD长为半径画弧交CB的延长线于点F，则图中阴影部分的面积是 .

答案解析收藏纠错 + 选题

三、解答题（共66分）

19. (2022九上·南宁月考) 计算：（-3）²÷（-2²+1）-（6-8）.

答案解析收藏纠错 + 选题
20. (2022九上·南宁月考) 先化简，再求值：（ $\text{[math]}$ ）÷ $\text{[math]}$ ，其中x＝ $\text{[math]}$ .

答案解析收藏纠错 + 选题
21. (2022九上·南宁月考) 如图，△ABC为等边三角形，△ABC绕点A逆时针旋转得△ACD，且BP＝CQ.
1. （1）求证：△ABP≌△ACQ；
2. （2）求∠APQ的度数.
答案解析收藏纠错 + 选题

22. (2022九上·南宁月考) 2020年南宁市开展创建全国文明城市活动，青秀区创城办招募了大量“卫生保洁”和“交通引导”志愿者（一人只参与一个项目），开展一段时间后，创城办决定派数位调查员分别调查这两个项目的开展情况.

（1）调查员小明被分配到调查“交通引导”项目的概率是；

（2）为掌握“交通引导”志愿志愿者早上7：20按时到位情况，小明对部分志愿者进行调查并整理，得到如下数据：

调查总人数	20	50	100	300	500
按时到位人数	18	46	94	283	472
按时到位频率	0.900	0.920	0.940	0.943	0.944

①分析上表中的数据，估算“交通引导”志愿者早上7：20按时到位的概率为（精确到0.01）；

②请估计4800名“交通引导”志愿者早上7：20能按时到位的人数.

答案解析收藏纠错 + 选题

23. (2022九上·南宁月考) “4G改变生活，5G改变社会”，不一样的5G手机给人们带来了全新的体验，某营业厅现有A、B两种型号的5G手机出售，售出1部A型、2部B型手机共获利1000元，售出2部A型、1部B型手机共获利800元.
1. （1）求A、B两种型号的手机每部利润各是多少元？
2. （2）若营业厅再次购进A、B两种型号手机共20部，其中B型手机的数量不超过A型手机数量的 $\text{[math]}$ ，请设计一个购买方案，使营业厅销售完这20部手机能获得最大利润，并求出这最大利润.
答案解析收藏纠错 + 选题
24. (2022九上·南宁月考) 如图1是一种手机平板支架，由托板、支撑板和底座构成，手机放置在托板上.图2是其侧面结构示意图，量得托板长AB＝120mm，支撑板长CD＝80mm，底座长DE＝90mm.托板AB固定在支撑板顶端点C处，且CB＝40mm，托板AB可绕点C转动，支撑板CD可绕点D转动.（参考数据，sin40°≈0.64，cos40°≈0.77，tan40°≈0.84，sin26.6°≈0.44，cos26.6°≈0.89，tan26.6°≈0.50， $\text{[math]}$ ）
1. （1）若∠DCB＝80°，∠CDE＝60°，求点A到直线DE距离；
2. （2）为了观看舒适，在（1）的情况下，把AB绕点C逆时针旋转10°后，再将CD绕点D顺时针旋转，使点B落在直线DE上，求CD旋转的角度.
答案解析收藏纠错 + 选题
25. (2022九上·南宁月考) 如图，抛物线经过A（-2，0），C（0，-3）两点，且对称轴为直线 $\text{[math]}$ .
1. （1）求抛物线的函数解析式；
2. （2）若直线y＝kx-5与抛物线交于点M，N，交x轴于点B，交y轴于点P，连接CN，且 $\text{[math]}$ .
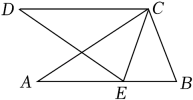
  ①求△CMN的面积；
  ②在平面内是否存在点一是E，使E，C，N，M四点能构成平行四边形，如果存在，请直接写出点E的坐标.
答案解析收藏纠错 + 选题
26. (2022九上·南宁月考) 如图，已知AC为⊙O的直径，连接AB，BC，OB，过点O作OE⊥AB于点E，点F是半径OC的中点，连接EF，BF.
1. （1）如图1，设⊙O的半径为2，若∠BAC＝30°，求线段EF的长.
2. （2）如图2，设BO交EF于点P，延长BO交⊙O于点D，连接DF.
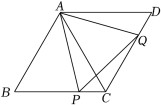
  ①求证：PE＝PF；
  ②若DF＝EF，求∠BAC的度数.
答案解析收藏纠错 + 选题