北京市丰台区2022~2023学年八年级上学期期末数学试卷

更新时间：2023-01-31 浏览次数：82 类型：期末考试

一、单选题

1. (2022八上·丰台期末) 下列四个图形分别是四届国际数学家大会的会标，其中不属于中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2023八下·海淀期末) 随着科技不断发展，芯片的集成度越来越高．我国企业中芯国际已经实现14纳米量产，14纳米等于0.000014毫米，将0.000014用科学记数法表示应为（）．

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024七下·章丘期末) 已知三角形的两边长分别为5cm和8cm，则第三边的长可以是（）

A . 2cm B . 3cm C . 6cm D . 13cm

答案解析收藏纠错 + 选题
4. (2022八上·丰台期末) 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024八下·渝北开学考) 等腰三角形的一个角是 $\text{[math]}$ ，它的底角的大小为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ 或 $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024八下·吴江月考) 若a≠b，则下列分式变形正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2022八上·丰台期末) 如图，在△ABC中，∠C=90°，∠A=30°，以点B为圆心，适当长为半径的画弧，分别交BA，BC于点M、N；再分别以点M、N为圆心，大于 $\text{[math]}$ MN的长为半径画弧，两弧交于点P，作射线BP交AC于点D，则下列说法中错误的是（）

A . BP是∠ABC的平分线 B . AD=BD C . $\text{[math]}$ D . CD= $\text{[math]}$ BD

答案解析收藏纠错 + 选题
8. (2022八上·丰台期末) 我们在观看台球比赛时，发现选手们常常会用反弹的技巧击打目标球．在此过程中，撞击路线与桌边的夹角等于反射路线与桌边的夹角，如图1， $\text{[math]}$ ．如图2，建立平面直角坐标系 $\text{[math]}$ ，已知A球位于点 $\text{[math]}$ 处，B球位于点 $\text{[math]}$ 处．现击打A球，使A球向桌边的整点位置（横纵坐标均为整数，球洞位置不可反弹）撞击，若A球最多在台球桌边反弹两次后击中B球，则满足条件的桌边整点有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题

9. (2024九下·光明模拟) 若 $\text{[math]}$ 有意义，则x的取值范围是．

答案解析收藏纠错 + 选题
10. (2022八上·丰台期末) 在平面直角坐标系 $\text{[math]}$ 中，点 $\text{[math]}$ 与点B关于x轴对称，则点B的坐标是．

答案解析收藏纠错 + 选题
11. (2022八上·丰台期末) 分解因式： $\text{[math]}$ ，

答案解析收藏纠错 + 选题
12. (2022八上·丰台期末) 如图，已知 $\text{[math]}$ ，请添加一个条件（不添加辅助线），使 $\text{[math]}$ ，依据是．

答案解析收藏纠错 + 选题
13. (2024八上·丰满期末) 若一个正多边形的每一个外角都是30°，则这个正多边形的边数为．

答案解析收藏纠错 + 选题
14. (2022八上·丰台期末) 如图1，在边长为a的大正方形中，剪去一个边长为3的小正方形，将余下的部分按图中的虚线剪开后，拼成如图2所示的长方形．根据两个图形阴影部分面积相等的关系，可以列出的等式为．

答案解析收藏纠错 + 选题
15. (2022八上·丰台期末) 如图， $\text{[math]}$ 是等边三角形 $\text{[math]}$ 的中线， $\text{[math]}$ ，则 $\text{[math]}$ 的度数为．

答案解析收藏纠错 + 选题
16. (2022八上·丰台期末) 欧拉是18世纪瑞士著名的数学家，他的贡献不仅遍及高等数学的各个领域，在初等数学中也留下了他的足迹．下面是关于分式的欧拉公式：
$\text{[math]}$

（其中a，b，c均不为零，且两两互不相等）．
1. （1）当 $\text{[math]}$ 时，常数p的值为．
2. （2）利用欧拉公式计算： $\text{[math]}$ ．
答案解析收藏纠错 + 选题

三、解答题

17. (2022八上·丰台期末) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2022八上·丰台期末) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
19. (2022八上·丰台期末) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
20. (2023八下·海淀期末) 已知：如图，点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 在同一直线上， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．求证： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
21. (2023八上·邯山期末) 先化简，再求值 $\text{[math]}$ ，其中x= $\text{[math]}$ ．

答案解析收藏纠错 + 选题
22. (2022八上·丰台期末) 解方程： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
23. (2022八上·丰台期末) 下面是小明同学设计的“作一个角等于已知角的2倍”的尺规作图的过程．
已知：如图1， $\text{[math]}$ ．
求作： $\text{[math]}$ ，使 $\text{[math]}$ ，且点D在射线 $\text{[math]}$ 上．
作法：
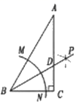
①如图2，在射线 $\text{[math]}$ 上任取一点C；
②作线段 $\text{[math]}$ 的垂直平分线 $\text{[math]}$ ，交 $\text{[math]}$ 于点D；
③连接 $\text{[math]}$ ．
则 $\text{[math]}$ 即为所求作的角．
根据上述作图过程，回答问题：
1. （1）用直尺和圆规，补全图2中的图形（保留作图痕迹）；
2. （2）完成下面的证明：
  证明： $\text{[math]}$ 是线段 $\text{[math]}$ 的垂直平分线，
  $\text{[math]}$ ▲ （）（填推理的依据）．
  $\text{[math]}$ （）（填推理的依据）．
  $\text{[math]}$ ，
  $\text{[math]}$ ．
答案解析收藏纠错 + 选题
24. (2022八上·丰台期末) 观察下列算式，完成问题：
算式①： $\text{[math]}$
算式②： $\text{[math]}$
算式③： $\text{[math]}$
算式④： $\text{[math]}$
……
1. （1）按照以上四个算式的规律，请写出算式⑤：；
2. （2）上述算式用文字表示为：“任意两个连续偶数的平方差都是4的奇数倍”．若设两个连续偶数分别为 $\text{[math]}$ 和 $\text{[math]}$ （ $\text{[math]}$ 为整数），请证明上述命题成立；
3. （3）命题“任意两个连续奇数的平方差都是4的奇数倍”是否成立？若成立，请证明；若不成立，请举出反例．
答案解析收藏纠错 + 选题

25. (2022八上·丰台期末) 小刚家近期准备换车，看中了价格相同的两款车，他对这两款车的部分信息做了调查，如下表所示：

燃油车	新能源车
油箱容积：40升	电池电量：60千瓦时
油价：9元/升	电价：0.6元/千瓦时
续航里程：a千米	续航里程：a千米
每千米行驶费用： $\text{[math]}$ 元	每千米行驶费用：____元

（续航里程指车辆在最大的能源储备下可连续行驶的总里程）

（1）表中的新能源车每千米行驶费用为元（用含a的代数式表示）；
（2）若燃油车的每千米行驶费用比新能源车多0.54元，分别求出两款车每千米行驶费用；
（3）在（2）的条件下，若燃油车和新能源车每年的其它费用分别为4800元和7500元．每年行驶里程至少超过千米时，使用新能源车的年费用更低（年费用=年行驶费用+年其它费用）．

答案解析收藏纠错 + 选题

26. (2022八上·丰台期末) 在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，射线 $\text{[math]}$ ， $\text{[math]}$ 的夹角为 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 于点 $\text{[math]}$ ，直线 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，连结 $\text{[math]}$ ．
1. （1）如图1，射线 $\text{[math]}$ ， $\text{[math]}$ 都在 $\text{[math]}$ 的内部．
  ①设 $\text{[math]}$ ，则 $\text{[math]}$ （用含有 $\text{[math]}$ 的式子表示）；
  ②作点 $\text{[math]}$ 关于直线 $\text{[math]}$ 的对称点 $\text{[math]}$ ，则线段 $\text{[math]}$ 与图1中已有线段的长度相等；
2. （2）如图2，射线 $\text{[math]}$ 在 $\text{[math]}$ 的内部，射线 $\text{[math]}$ 在 $\text{[math]}$ 的外部，其他条件不变，用等式表示线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的数量关系，并证明．
答案解析收藏纠错 + 选题
27. (2023八上·北京市期中) 在平面中，对于点M，N，P，若 $\text{[math]}$ ，且 $\text{[math]}$ ，则称点P是点M和点N的“垂等点”．在平面直角坐标系 $\text{[math]}$ 中，
1. （1）已知点 $\text{[math]}$ ，点 $\text{[math]}$ ，则点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 中是点M和点N的“垂等点”的是；
2. （2）已知点 $\text{[math]}$ ， $\text{[math]}$ ．
  ①若在第二象限内存在点C，使得点B是点A和点C的”垂等点”，写出点C的坐标（用含b的式子表示），并说明理由；
  ②当 $\text{[math]}$ 时，点D，点E是线段 $\text{[math]}$ ， $\text{[math]}$ 上的动点（点D，点E不与点A，B，O重合）．若点F是点D和点E的”垂等点”，直接写出点F的纵坐标t的取值范围．
答案解析收藏纠错 + 选题