2023年浙教版数学七年级下册全方位训练卷第二章二元一次方...

更新时间：2023-01-12 浏览次数：265 类型：单元试卷

一、单选题（每题3分，共30分）

1. (2023七下·杭州期中) 若 $\text{[math]}$ +（m-1）y=6是关于x，y的二元一次方程，则m的值是（）

A . 3 B . 1 C . 任意数 D . 1或3

答案解析收藏纠错 + 选题
2. (2023七下·乌鲁木齐期中) 若 $\text{[math]}$ 是二元一次方程 $\text{[math]}$ 的一个解，则下列x，y的值也是该方程的解的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. 使方程组 $\text{[math]}$ 有自然数解的整数m（）

A . 只有5个 B . 只能是偶数 C . 是小于16的自然数 D . 是小于32的自然数

答案解析收藏纠错 + 选题
4. (2022七下·西宁期末) 已知 $\text{[math]}$ 、 $\text{[math]}$ 互补， $\text{[math]}$ 比 $\text{[math]}$ 小 $\text{[math]}$ ，设 $\text{[math]}$ 、 $\text{[math]}$ 的度数分别为 $\text{[math]}$ 、 $\text{[math]}$ ，下列方程组中正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2022七下·井研期末) 若a、b、c、d是正整数，且a+b＝20，a+c＝24，a+d＝22，设a+b+c+d的最大值为M，最小值为N，则M﹣N＝（）

A . 28 B . 12 C . 48 D . 36

答案解析收藏纠错 + 选题
6. (2020七下·余杭期末) 我国古代数学家张丘建在《张丘建算经）里，提出了“百钱买百鸡”这个有名的数学问题.用100个钱买100只鸡，公鸡每只五个钱，母鸡每只三个钱，小鸡每个钱三只.问公鸡，小鸡各买了多少只？在这个问题中，小鸡的只数不可能是（）

A . 87 B . 84 C . 81 D . 78

答案解析收藏纠错 + 选题
7. (2021七下·昭通期末) 已知关于 $\text{[math]}$ ， $\text{[math]}$ 的方程组 $\text{[math]}$ ，给出下列说法：①当 $\text{[math]}$ 时，方程组的解也是方程 $\text{[math]}$ 的一个解；②当 $\text{[math]}$ 时， $\text{[math]}$ ；③不论 $\text{[math]}$ 取什么实数， $\text{[math]}$ 的值始终不变；④若 $\text{[math]}$ ，则 $\text{[math]}$ 以上四种说法中正确的有（）个

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
8. (2022七下·怀仁期末) 一道来自课本的习题：
从甲地到乙地先有一段上坡路后有一段平路．如果保持上坡每小时走3km，平路每小时走4km，下坡每小时走5km，那么从甲地到乙地需54分钟，从乙地到甲地需42分钟，甲地到乙地全程是多少？
小红将这个实际问题转化为二元一次方程组问题，采用间接设法：
设坡路有x km，平路有y km，则全程为（x＋y）km．已经列出一个方程 $\text{[math]}$ ，则另一个方程正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2021七下·桥西期末) 将两块完全相同的长方体木块先按图1的方式放置，再按图2的方式放置，测得的数据如图所示．则桌子的高度 $\text{[math]}$ （）

A . 70 B . 55 C . 40 D . 30

答案解析收藏纠错 + 选题
10. (2022七下·滨城期末) 如图，长青化工厂与 $\text{[math]}$ ， $\text{[math]}$ 两地有公路、铁路相连．这家工厂从 $\text{[math]}$ 地购买一批每吨1000元的原料运回工厂，制成每吨6000元的产品运到 $\text{[math]}$ 地．公路运价为1.6元 $\text{[math]}$ ，铁路运价为1.2元 $\text{[math]}$ ，这两次运输共支出公路运费16000元，铁路运费97200元．这批产品的销售款比原料费与运输费的和多（）元．

A . 1286800 B . 299000 C . 1286000 D . 298000

答案解析收藏纠错 + 选题

二、填空题（每题3分，共15分）

11. (2022七下·海陵期中) 小亮解方程组 $\text{[math]}$ 的解为 $\text{[math]}$ ，由于不小心，滴上了两滴墨水，刚好遮住了两个数●和★，请你帮他找回★和●，这个数★＝，●＝.

答案解析收藏纠错 + 选题
12. (2021七下·丽水期中) 若关于x ， y的 $\text{[math]}$ 的解是 $\text{[math]}$ ，则关于m ， n的方程组 $\text{[math]}$ 的解是．

答案解析收藏纠错 + 选题
13. (2021七下·开学考) 为迎接建国70周年，某商店购进 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三种纪念品共若干件，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三种纪念品的数量之比为8：7：9，一段时间后，根据销售情况，补充三种纪念品后，库存总数量比第一次多200件，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三种纪念品的比例为9：10：10，又一段时间后，根据销售情况，再次补充三种纪念品，库存总数景比第二次多170 件，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三种纪念品的比例为7： 6： 6，已知第一次三种纪念品总数盘不超过1000件，则第一次购进 $\text{[math]}$ 种纪念品件.

答案解析收藏纠错 + 选题
14. (2018七上·鄞州期中) 如图，两个形状、大小完全相同的大长方形内放入四个如图③的小长方形后分别得到如图①、图②、已知大长方形的长为a，则图②阴影部分周长与图①阴影部分周长的差是．

答案解析收藏纠错 + 选题
15. (2022七下·上虞期末) 小明在拼图时，发现8个一样大小的长方形如图1那样，恰好可以拼成一个大的长方形．小红看见了，说：“我来试一试．”结果小红七拼八凑，拼成如图2那样的正方形．“咳，怎么中间还留了一个洞，恰好是边长为 $\text{[math]}$ 的小正方形 $\text{[math]}$ ”请你写出这些长方形的长和宽．

答案解析收藏纠错 + 选题

三、计算题（共8分）

16. (2021七下·古浪月考) 解方程组
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$
3. （3） $\text{[math]}$ ；
4. （4） $\text{[math]}$
答案解析收藏纠错 + 选题

四、解答题（共8题，共67分）

17. (2020七下·下城期末) 关于x，y的二元一次方程ax+by＝c（a，b，c是常数），b＝a+1，c＝b+1.
1. （1）当 $\text{[math]}$ 时，求c的值.
2. （2）当a＝ $\text{[math]}$ 时，求满足|x|＜5，|y|＜5的方程的整数解.
3. （3）若a是正整数，求证：仅当a＝1时，该方程有正整数解.
答案解析收藏纠错 + 选题
18. (2019七下·余杭期末) 已知关于x，y的二元一次方程组 $\text{[math]}$ （a为实数）．
1. （1）若方程组的解始终满足y=a+1，求a的值．
2. （2）已知方程组的解也是方程bx+3y=1(b为实数，b≠0且b≠-6)的解．
  ①探究实数a，b满足的关系式．
  
  ②若a，b都是整数，求b的最大值和最小值．
答案解析收藏纠错 + 选题
19. (2017七下·顺义期末)
1. （1）阅读下列材料并填空：
  对于二元一次方程组 $\text{[math]}$ 我们可以将x，y的系数和相应的常数项排成一个数表 $\text{[math]}$ ，求得的一次方程组的解 $\text{[math]}$ 用数表可表示为 $\text{[math]}$ .用数表可以简化表达解一次方程组的过程如下，请补全其中的空白：
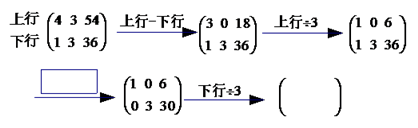
  从而得到该方程组的解为 $\text{[math]}$
2. （2）仿照（1）中数表的书写格式写出解方程组 $\text{[math]}$ 的过程．
答案解析收藏纠错 + 选题
20. 已知关于x，y的方程组 $\text{[math]}$ 的解是 $\text{[math]}$
1. （1）若把x换成m，y换成n，得到的关于m，n的方程组为 $\text{[math]}$ ，则这个方程组的解是 $\text{[math]}$ .
2. （2）若把x换成2x，y换成3y，得到方程组 $\text{[math]}$ ，则 $\text{[math]}$ ，所以这个方程组的解是 .
3. （3）根据以上的方法解方程组 $\text{[math]}$
答案解析收藏纠错 + 选题
21. (2023七下·临潼期末) 阅读下列材料：
小明同学遇到下列问题：解方程组 $\text{[math]}$ 小明发现如果用代入消元法或加减消元法求解，运算量比较大，容易出错．如果把方程组中的（2x+3y）看成一个整体，把（2x﹣3y）看成一个整体，通过换元，可以解决问题．以下是他的解题过程：令m＝2x+3y，n＝2x﹣3y．原方程组化为 $\text{[math]}$ ，解的 $\text{[math]}$ ，把 $\text{[math]}$ 代入m＝2x+3y，n＝2x﹣3y，得 $\text{[math]}$ 解得 $\text{[math]}$ 所以，原方程组的解为 $\text{[math]}$ ．
请你参考小明同学的做法解方程组：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
22. (2020七下·温州期中) 文雅书店出售A，B两种书籍，已知A书籍单售为每本50元，B书籍单售为每本30元，整套(A，B各一本)出售为每套70元。
1. （1）小明购买了A，B两种书籍共20本，且购买的B书籍数量比A书籍数量的2倍少4本。
  ①小明购买了A，B两种书籍各多少本？
  
  ②小明至少需要花费多少钱？
2. （2）如果小刚花了600元购买A，B两种书籍，其中A书籍购买了8本，那么有哪几种购买方案？其中哪一种方案最划算？
答案解析收藏纠错 + 选题
23. (2019七下·长兴月考) 某校举办“迎冬奥会“学生书画展览，现要在长方形展厅中划出3个形状、大小完全一样的小长方形(图中阴影部分)区域摆放作品．
1. （1）如图1，若大长方形的长和宽分别为45米和30米，设小长方形的长为x，宽为y，求出x和y的值．
2. （2）如图2，若大长方形的长和宽分别为a和b．
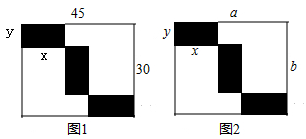
  ①求出1个小长方形周长与大长方形周长之比；
  
  ②若作品展览区域(阴影部分)面积占展厅面积的 $\text{[math]}$ ，求x和y的数量关系．
答案解析收藏纠错 + 选题
24. 某包装生产企业承接了一批礼品盒制作业务，为了确保质量，该企业进行试生产.他们购得规格是170cm×40cm的标准板材作为原材料，每张标准板材再按照裁法一或裁法二裁下A型与B型两种板材（不计损耗），如图1.（单位：cm）
1. （1）列出方程（组），求出图1中a与b的值；
2. （2）在试生产阶段，若将30张标准板材用裁法一裁剪，4张标准板材用裁法二裁剪，再将得到的A型与B型板材做侧面和底面，做成图2的竖式（高大于长）与横式（长大于高）两种无盖礼品盒.
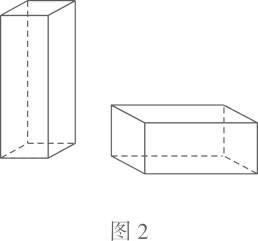
  ①两种裁法共生产A型板材 ▲ 张，B型板材 ▲ 张.
  
  ②能否在做成若干个上述的两种无盖礼品盒后，恰好把①中的A型板材和B型板材用完？若能，则竖式无盖礼品盒与横式无盖礼品盒分别做了几个？若不能，则最多能做成竖式和横式两种无盖礼品盒共多少个？并直接写出此时做成的横式无盖礼品盒的个数.
答案解析收藏纠错 + 选题