10.
(2023高三上·丰台期末)
市场占有率指在一定时期内，企业所生产的产品在其市场的销售量（或销售额）占同类产品销售量（或销售额）的比重．一般来说，市场占有率会随着市场的顾客流动而发生变化，如果市场的顾客流动趋向长期稳定，那么经过一段时期以后的市场占有率将会出现稳定的平衡状态（即顾客的流动，不会影响市场占有率），此时的市场占有率称为“稳定市场占有率”．有A，B，C三个企业都生产某产品，2022年第一季度它们的市场占有率分别为：40%，30%，30%．经调查，2022年第二季度A，B，C三个企业之间的市场占有率转移情况如下图所示：
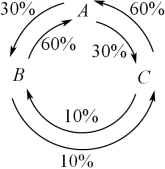
若该产品以后每个季度的市场占有率转移情况均与2022年第二季度相同，则当市场出现稳定的平衡状态，最终达到“稳定市场占有率”时，A企业该产品的“稳定市场占有率”为（ ）
