 B .
B .  C .
C . 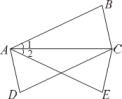
①把沿直线
翻折180°,可得到
;
②把沿线段
的垂直平分线翻折180°,可得到
;
③把沿射线DC方向平移与
相等的长度,可得到
.
其中所有符合题意结论的序号是( )

区间段 | 区间近似里程 | 区间设计最高时速 | 相应所用时间 |
北京城市副中心站−香河站 | 47.8 | t1 | |
香河站−唐山西站 | 87 | v | t2 |


分析:如图1所示,之前我们学过“推”三角尺画平行线,这种画法的实物操作图可以启发我们预设目标示意图,分析尺规作图思路.

①请参考以上内容完成尺规作图,保留作图痕迹,不必写作法;
②在①中用到的判定的依据是.
求作:凸四边形 , 使得
, 且
为等腰三角形.

请完成尺规作图并写出所求作的四边形,保留作图痕迹,不必写作法.
①小明画出图1并猜想 . 同学小亮说“要让你这个结论成立,需要增加条件:
▲ °.”
请写出小亮所说的条件;
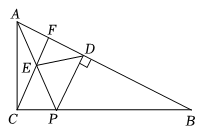
②小明重新画出图2并猜想 . 他证明的简要过程如下:

请你判断小明的证明是否正确并说明理由;
①借助小明画出的图2证明;
②延长到F,使
, 连结
. 补全图形,猜想
与
的数量关系并加以证明.

多边形 | 面积S | 内部格点数N | 边上格点数L | |
Ⅰ | ||||
Ⅱ | 7 | 4 | 8 | 8 |
Ⅲ | ||||
Ⅳ | 9 | 5 | 10 | 10 |
Ⅴ | 11 | 11 |
a.小明在做分式运算时发现如下一个等式,并对它进行了证明.
①
b.小明尝试写出了符合这个特征的其他几个等式:
②
③
④
c.小明邀请同学小亮根据上述规律写出第⑤个等式和第n个等式(用含n的式子表示,n为正整数);
d.小亮对第n个等式进行了证明.
解答下列问题:
①如果点的2倍关联点M在x轴上,那么点M的坐标为;
②如果点是点
的k倍关联点,且满足
,
, 那么整数k的最大值为;