日期 | 12月12日 | 12月13日 | 12月14日 | 12月15日 | 12月16日 |
最高气温 | |||||
日期 | 12月17日 | 12月18日 | 12月19日 | 12月20日 | 12月21日 |
最高气温 |
在这天中,最高气温为
出现的频率是( )
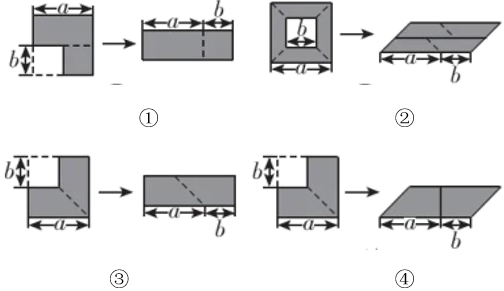



解答下列问题:

请你根据统计图提供的信息,解答下列问题:

在等腰三角形纸片中,
,
. 现要将其剪成三张小纸片,使每张小纸片都是等腰三角形(不能有剩余).下面是小文借助尺规解决这一问题的过程,请阅读后完成相应的任务.
作法:如图1. ①分别作 ②连接
结论:沿线段 理由:∵点P在线段 ∴____.(依据) 同理,得 ∴ ∴ |
任务:


