
B .
B . 
C .
C . 
D .
D . 



 D .
D . 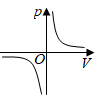 B .
B . 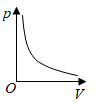 C .
C .  D .
D . 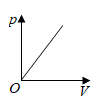


解:去分母,得: .
去括号,得: .
移项,合并同类项,
解得: .
请你分析上面圆圆同学的解答过程是否有错误?如果有错误,写出错误原因以及正确的解答过程.

小专题“图形的剪拼”
今天我们研究特殊四边形的时候发现,如果将其沿对角线裁剪后,得到的四个三角形可以拼成很多新的图形.我们设计做以下一些尝试.
图1是一张边长为2的正方形纸片,将其沿对角线剪开,得到图2所示四个全等的等腰直角三角形.用这四张纸片,重新摆放,可以得到特殊的图形.
操作一:奋进组接如图3所示的方式摆放,得到正方形 .
操作二:智慧组按如图4所示的方式摆放,得到正方形 .
操作三:如图5,将菱形沿对角线剪开,得到四个全等的直角三角形,无缝隙、不重叠地拼成一个矩形.





①请你用图5所得到的四个全等三角形无缝隙不重叠地拼出一个矩形;
②在菱形中,若
,
. 在①中,你拼成的矩形的对角线长为 ▲ .