





请完成下列推理过程:
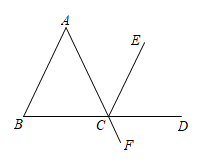
证明:∵CD 平分∠ECF
∴∠ECD= ▲ ( )
∵∠ACB=∠FCD( )
∴∠ECD=∠ACB( )
∵∠B=∠ACB
∴∠B=∠▲( )
∴ ( ).

完成推理过程:
BE平分∠ABD(已知),
∴∠ABD=2∠α( ).
∵DE平分∠BDC(已知),
∴∠BDC=2∠β( )
∴∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β)( )
∵∠α+∠β=90°(已知),
∴∠ABD+∠BDC=180°( ).
∴AB∥CD( ).
如图,E,F分别在AB和CD上, ,
与
互余,
于G.
求证: .

证明:∵ , ∴
( ),
∵(已知),∴ ▲
▲ ( ),
∴( ),
∵(平角的定义),∴
.
∵与
互余(已知),∴
(互余的定义),
∴( ),∴
( ).
已知,如图,直线AB,CD被直线EF所截,点H为CD与EF的交点,GH⊥CD于点H,∠2=30°,∠1=60°.试说明: .
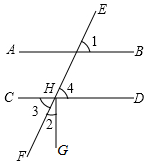
解:∵GH⊥CD( ),
∴∠CHG=90°( ).
又∵∠2=30°( ),
∴∠3=( ).
∴∠4=60°( ).
又∵∠1=60°( ),
∴∠1=∠4( ).
∴( ).


②若∠ACB=140°,求∠DCE ;
若存在,请直接写出∠ACE的所有可能的值(不必说明理由);若不存在,请说明理由.

