2023年苏科版数学八年级下册全方位训练卷9.4矩形、菱形、...

更新时间：2023-02-21 浏览次数：59 类型：同步测试

一、单选题（每题3分，共24分）

1. (2022八下·溧阳期末) 下列命题中，是真命题的是（）

A . 有一个角是直角的四边形是矩形 B . 对角线相等的平行四边形是菱形 C . 一组邻边相等的平行四边形是菱形 D . 四边都相等的四边形是正方形

答案解析收藏纠错 + 选题
2. (2023九上·高台月考) 如图，已知四边形 $\text{[math]}$ 是平行四边形，对角线 $\text{[math]}$ 交于点 $\text{[math]}$ ，则下列结论中错误的是（）

A . 当 $\text{[math]}$ 时，它是菱形 B . 当 $\text{[math]}$ 时，它是正方形 C . 当 $\text{[math]}$ 时，它是矩形 D . 当 $\text{[math]}$ 时，它是菱形

答案解析收藏纠错 + 选题
3. (2024八下·祁东期末) 下面性质中矩形具有而菱形没有的是（）

A . 对角线相等 B . 邻边相等 C . 对角线垂直 D . 对边相等

答案解析收藏纠错 + 选题
4. (2021八下·北京期末) 若菱形的两条对角线的长分别为6和10，则菱形的面积为（）

A . 15 B . 24 C . 30 D . 60

答案解析收藏纠错 + 选题
5. (2022八下·启东月考) 在矩形ABCD中，对角线AC，BD相交于点O，∠AOD=60°，OB=2cm，那么矩形ABCD的面积为（）

A . $\text{[math]}$ cm B . 2 $\text{[math]}$ cm C . 3 $\text{[math]}$ cm D . 4 $\text{[math]}$ cm

答案解析收藏纠错 + 选题
6. (2022八下·启东月考) 如图，若四边形ABCD是菱形，AC=24，BD=10，则菱形ABCD的边长是（）

A . 13 B . 12 C . 26 D . 52

答案解析收藏纠错 + 选题
7. (2022八下·溧阳期末) 如图，把正方形纸片ABCD沿对边中点所在直线折叠后展开，折痕为MN；再过点D折叠，使得点A落在MN上的点F处，折痕为DE，则 $\text{[math]}$ 的值是（）

A . $\text{[math]}$ B . $\text{[math]}$ －1 C . 2－ $\text{[math]}$ D . 3－ $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2020八下·淮安期末) 正方形ABCD中，对角线AC、BD交于点O，则∠CBO等于（）

A . 30° B . 45° C . 60° D . 75°

答案解析收藏纠错 + 选题

二、填空题（每题3分，共24分）

9. (2022八下·广陵期末) 如图，矩形ABCD的对角线AC、BD相交于点O，∠BOC＝120°，AC＝6．则AB＝．

答案解析收藏纠错 + 选题
10. (2023八下·尧都期末) 如图，过四边形ABCD的四个顶点分别作对角线AC、BD的平行线，若所围成的四边形EFGH是矩形，则原四边形ABCD需满足的条件是.（只需写出一个符合要求的条件）

答案解析收藏纠错 + 选题
11. (2022八下·泰兴期末) 在矩形ABCD中，对角线AC、BD相交于点O，AO＝6cm，则BD＝cm．

答案解析收藏纠错 + 选题
12. (2022八下·沭阳期末) 菱形的两条对角线长分别是 $\text{[math]}$ 和 $\text{[math]}$ ，则菱形的周长是 $\text{[math]}$ .

答案解析收藏纠错 + 选题
13. (2022八下·盐城期末) 已知一个菱形的边长为 $\text{[math]}$ ，其中一条对角线长为 $\text{[math]}$ ，则这个菱形的面积为.

答案解析收藏纠错 + 选题
14. (2022八下·南京期末) 如图，正方形 $\text{[math]}$ 在第一象限，点 $\text{[math]}$ 、 $\text{[math]}$ ，则点 $\text{[math]}$ 的坐标是．（用含 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 的代数式表示）

答案解析收藏纠错 + 选题
15. (2022八下·江都期中) 如图，正方形 $\text{[math]}$ 和正方形 $\text{[math]}$ 的边长分别为4和2，正方形 $\text{[math]}$ 绕点C旋转，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. (2022八下·常熟期末) 如图，木制活动衣帽架由三个全等的菱形构成，在 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 处安装上、下两排挂钩，可以根据需要改变挂钩间的距离，并在 $\text{[math]}$ ， $\text{[math]}$ 处固定.已知菱形 $\text{[math]}$ 的边长为13cm，要使两排挂钩间的距离 $\text{[math]}$ 为24cm，则 $\text{[math]}$ ， $\text{[math]}$ 之间的距离（即线段 $\text{[math]}$ 的长）为cm.

答案解析收藏纠错 + 选题

三、作图题（共10分）

17. (2022八下·北仑期末) 如图1、2都是边长为1的全等菱形组成的网格图，网格的交点称为格点，AB是端点落在格点上的线段，请仅用无刻度直尺作出符合下列要求的格点四边形．
1. （1）请在图1中作出一个以AB为边的平行四边形（非矩形）．
2. （2）请在图2中作出一个以AB为边的矩形．
答案解析收藏纠错 + 选题

四、解答题（共8题，共62分）

18. (2020八下·淮安期中) 已知：如图，在正方形ABCD中，点P是对角线BD上一点，PM⊥AD，PN⊥AB，垂足分别为M、N.求证：MN=PC.

答案解析收藏纠错 + 选题
19. (2023八下·浏阳期中) 如图，菱形ABCD的对角线AC、BD相交于点O， $\text{[math]}$ ， $\text{[math]}$ ，OE与AB交于点F.
1. （1）求证：四边形AEBO为矩形；
2. （2）若OE＝10，AC＝16，求菱形ABCD的面积.
答案解析收藏纠错 + 选题
20. (2022八下·苏州期中) 如图，已知菱形ABCD的对角线相交于点O，延长AB至点E，使BE＝AB，连接CE．
1. （1）求证：BD＝EC；
2. （2）当∠DAB为多少度时，四边形BECD为菱形？并说明理由．
答案解析收藏纠错 + 选题
21. (2022·南通模拟) 操作：第一步：如图1，对折长方形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展开.
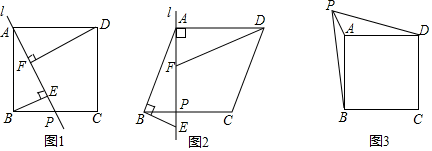
第二步：如图2，再一次折叠纸片，使点A落在EF上的N处，并使折痕经过点B，得到折痕BM，同时得到线段BN.连结AN，易知△ABN的形状是 ▲ .
论证：如图3，若延长MN交BC于点P，试判定△BMP的形状，请说明理由.

答案解析收藏纠错 + 选题
22. (2022八下·淮安期末) 如图，平行四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ .对角线 $\text{[math]}$ ， $\text{[math]}$ 相交于点 $\text{[math]}$ ，将直线 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ ，分别交直线 $\text{[math]}$ 、 $\text{[math]}$ 于点 $\text{[math]}$ 、 $\text{[math]}$ .
1. （1）当 $\text{[math]}$ °，四边形 $\text{[math]}$ 是平行四边形；
2. （2）在旋转的过程中，从 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 中任意找4个点为顶点构造四边形.
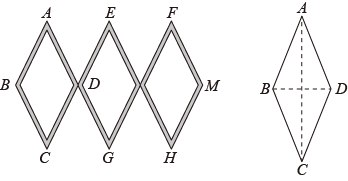
  ① $\text{[math]}$ ▲ °，构造的四边形是菱形；
  
  ②若构造的四边形是矩形，则不同的矩形应该有 ▲ 个.
答案解析收藏纠错 + 选题
23. (2022八下·盐城期末) 如图1，在边长为4的正方形ABCD中，点E为对角线BD上一点，连接AE，过点E作 $\text{[math]}$ ，交边CD于点F，若 $\text{[math]}$ ，求BE的长.
下面是小明、小华和小东三位同学关于本题不同视角下的部分思维过程：

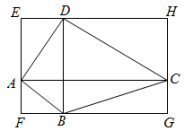
小明：从直线BD是正方形的对称轴角度看，连接EC，如图2，则 $\text{[math]}$ ， ∠ECD＝∠EAD，又 $\text{[math]}$ ， ……

小华：从 $\text{[math]}$ 的角度看，可以过点E作BC的平行线，交AB、CD于M、N，如图3，通过证明 $\text{[math]}$ ， ……

小东：从 $\text{[math]}$ 的角度看，还可以过点E作BD的垂线，交DC的延长线于点P，如图4，……

请结合上面的思路，求BE的长.

答案解析收藏纠错 + 选题
24. (2022八下·广陵期末) 问题情境：
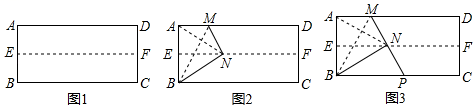
如图①，点E为正方形ABCD内一点，∠AEB＝90°，将Rt△ABE绕点B按顺时针方向旋转90°，得到△CBE′（点A的对应点为点C）．延长AE交CE′于点F，连接DE．
1. （1）猜想证明：
  试判断四边形BE'FE的形状，并说明理由；
2. （2）如图②，若DA＝DE，请猜想线段CF与 $\text{[math]}$ 的数量关系并加以证明；
3. （3）解决问题：
  如图①，若AB＝4，当BE的长为时，△ADE为等腰三角形，请直接写出结果．
答案解析收藏纠错 + 选题
25. (2022八下·广陵期中)
1. （1）【方法回顾】
  如图1，过正方形ABCD的顶点A作一条直线l交边BC于点P，BE⊥AP于点E，DF⊥AP于点F，若DF＝2.5，BE＝1，则EF＝．
2. （2）【问题解决】
  如图2，菱形ABCD的边长为1.5，过点A作一条直线l交边BC于点P，且∠DAP＝90°，点F是AP上一点，且∠BAD+∠AFD＝180°，过点B作BE⊥AB，与直线l交于点E，若EF＝1，求BE的长．
3. （3）【思维拓展】
  如图3，在正方形ABCD中，点P在AD所在直线上的上方，AP＝2，连接PB，PD，若△PAD的面积与△PAB的面积之差为m（m＞0），则PB²﹣PD²的值为．（用含m的式子表示）
答案解析收藏纠错 + 选题