江苏省扬州市广陵区2021-2022学年八年级下学期期中数学...

更新时间：2022-09-15 浏览次数：84 类型：期中考试

一、单选题

1. (2022八下·广陵期中) 剪纸是扬州的非物质文化遗产之一，下列剪纸作品中是中心对称图形的是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2022八下·广陵期中) 下列调查中，最适宜采用普查方式的是（）

A . 对全国初中学生视力状况的调査 B . 了解江苏省义务教育阶段男女学生比例情况 C . 旅客上飞机前的安全检查 D . 了解某种品牌手机电池的使用寿命

答案解析收藏纠错 + 选题
3. (2022八下·广陵期中) 下列统计图中，可以直观地反映出数据变化的趋势的统计图是（）

A . 折线图 B . 扇形图 C . 条形图 D . 频数分布直方图

答案解析收藏纠错 + 选题
4. (2022八下·广陵期中) 成语“守株待兔”所描述的事件是（）

A . 必然事件 B . 随机事件 C . 不可能事件 D . 无法确定

答案解析收藏纠错 + 选题
5. (2022八下·广陵期中) 无论x取什么数时，总是有意义的分式是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022八下·广陵期中) 把分式 $\text{[math]}$ 中的x和y都扩大3倍，则分式的值（）

A . 不变 B . 扩大为原来的3倍 C . 缩小为原来的 $\text{[math]}$ D . 扩大为原来的9倍

答案解析收藏纠错 + 选题
7. (2022八下·广陵期中) 如图，在正方形ABCD外侧，作等边三角形ADE，AC，BE相交于点F，则∠BFC为（）

A . 75° B . 60° C . 55° D . 45°

答案解析收藏纠错 + 选题
8. (2022八下·广陵期中) 如图，在▱ABCD中，AD＝2AB ， F是AD的中点，作CE⊥AB ，垂足E在线段AB上，连接EF、CF ，下列结论中：①∠DCF＝ $\text{[math]}$ ∠BCD；②∠DFE＝3∠AEF；③EF＝CF；④S_△BEC＝S_△CEF ．一定成立的是（）

A . ①②③④ B . ①②③ C . ①②④ D . ①③④

答案解析收藏纠错 + 选题

二、填空题

9. (2022八下·任丘期末) 为了解新冠肺炎疫情解封后刚复学时学生的心理健康，扬州市某区在全区7600名初中同学中随机抽查了500名同学进行问卷调查，对500个数据进行整理，在频数的统计表中各组的频数之和等于．

答案解析收藏纠错 + 选题
10. (2022八下·广陵期中) 样本的50个数据分别落在4个组内，第1、2、3组数据的个数分别是7、8、15，则落在第4组数据的频数为．

答案解析收藏纠错 + 选题
11. (2023·深圳模拟) 大数据分析技术为打赢疫情防控阻击战发挥了重要作用.如图是小明同学的苏康码（绿码）示意图，用黑白打印机打印于边长为2cm的正方形区域内，为了估计图中黑色部分的总面积，在正方形区域内随机掷点，经过大量重复试验，发现点落入黑色部分的频率稳定在0.6左右，据此可以估计黑色部分的总面积约为 $\text{[math]}$ .

答案解析收藏纠错 + 选题
12. (2022八下·广陵期中) 若分式 $\text{[math]}$ 的值为负数，则x的取值范围是．

答案解析收藏纠错 + 选题
13. (2022八下·广陵期中) 如果 $\text{[math]}$ ，则 $\text{[math]}$ =．

答案解析收藏纠错 + 选题
14. (2022八下·广陵期中) 如图，▱ABCD中，AC、BD相交于点O，若AD=6，AC+BD=16，则△BOC的周长为.

答案解析收藏纠错 + 选题
15. (2024九下·海南模拟) 已知菱形的周长为20，一条对角线长为8，则菱形的面积为．

答案解析收藏纠错 + 选题
16. (2022八下·广陵期中) 如图，△ABC为钝角三角形，将△ABC绕点A按逆时针方向旋转120°得到△AB′C′，连接BB′，若AC′∥BB′，则∠C′AB′的度数为．

答案解析收藏纠错 + 选题
17. (2023八下·北辰期中) 如图，矩形纸片ABCD中，已知AD=8，折叠纸片使AB边与对角线AC重合，点B落在点F处，折痕为AE，且EF=3，则AB的长为．

答案解析收藏纠错 + 选题
18. (2022八下·广陵期中) 如果记 $\text{[math]}$ =f（x），并且f（1）表示当x=1时y的值，即f（1）= $\text{[math]}$ ；f（ $\text{[math]}$ ）表示，当x= $\text{[math]}$ 时y的值，即f（ $\text{[math]}$ ）= $\text{[math]}$ ；那么f（1）+f（2）+f（ $\text{[math]}$ ）+f（3）+f（ $\text{[math]}$ ）+…+f（2021）+f（ $\text{[math]}$ ）+f（2022）+f（ $\text{[math]}$ ）=．

答案解析收藏纠错 + 选题

三、解答题

19. (2022八下·广陵期中) 如图，平行四边形ABCD中，E、F分别是边BC、AD的中点，求证：∠ABF=∠CDE．

答案解析收藏纠错 + 选题

20. (2022八下·广陵期中) 在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个，小颖做摸球实验，她将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程，下表是实验中的一组统计数据：

摸球的次数 $\text{[math]}$	100	200	300	500	800	1000	3000
摸到白球的次数 $\text{[math]}$	65	124	178	302	481	599	1803
摸到白球的频率 $\text{[math]}$	0.65	0.62	0.59	0.604	0.601	0.599	0.601

（1）请估计：当n很大时，摸到白球的频率将会接近（精确到0.1）
（2）假如你摸一次，你摸到白球的概率P（白球）=．
（3）试估算盒子里黑、白两种颜色的球各有多少只？

答案解析收藏纠错 + 选题

21. (2023九下·句容月考) 扬州教育推出的“智慧学堂”已成为同学们课外学习的得力助手.为了解同学们“智慧学堂”平台使用的熟练程度，某校随机抽取了部分同学进行调查，并将调查结果绘制成如下两幅尚不完整的统计图.

根据以上信息，回答下列问题：
1. （1）本次调查的样本容量是，扇形统计图中表示A等级的扇形圆心角为 $\text{[math]}$ ；
2. （2）补全条形统计图；
3. （3）学校拟对“不太熟练或不熟练”的同学进行平台使用的培训，若该校有2000名学生，试估计该校需要培训的学生人数.
答案解析收藏纠错 + 选题
22. (2022八下·广陵期中) 如图，在正方形网格中，△AOB的顶点均在格点上点A、B的坐标分别是A（3，2）、B（1，3）．
1. （1）点A关于点O中心对称点的坐标为；
2. （2） △AOB绕点O顺时针旋转90°后得到△A₁OB₁ ，在方格纸中画出△A₁OB₁ ，并写出点B₁的坐标 ▲ ；
3. （3）在y轴上找一点P，使得PA+PB最小，请在图中标出点P的位置，并求出这个最小值．
答案解析收藏纠错 + 选题
23. (2022八下·会东月考) 已知：如图，E、F是▱ABCD的对角线AC上的两点，AE=CF．
求证：
1. （1） △ADF≌△CBE；
2. （2） EB∥DF．
答案解析收藏纠错 + 选题
24. (2022八下·广陵期中) 如图， $\text{[math]}$ 的对角线AC，BD相交于点O，过点O作 $\text{[math]}$ ，分别交AB，DC于点E、F，连接AF、CE.
1. （1）若 $\text{[math]}$ ，求EF的长；
2. （2）判断四边形AECF的形状，并说明理由.
答案解析收藏纠错 + 选题
25. (2024八下·南昌期中) 在 $\text{[math]}$ ABCD，过点D作DE⊥AB于点E，点F在边CD上，DF＝BE，连接AF，BF.
1. （1）求证：四边形BFDE是矩形；
2. （2）若CF＝3，BF＝4，DF＝5，求证：AF平分∠DAB．
答案解析收藏纠错 + 选题
26. (2022八下·广陵期中) 阅读下面材料：
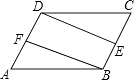
在数学课上，老师请同学思考如下问题：如图1，我们把一个四边形ABCD的四边中点E，F，G，H依次连接起来得到的四边形EFGH是平行四边形吗.

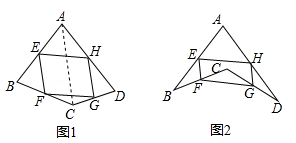
小敏在思考问题时，有如下思路：连接AC.

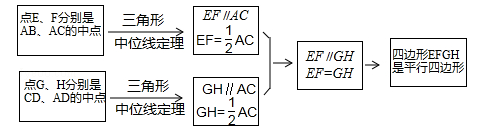
结合小敏的思路作答：
1. （1）若只改变图1中四边形ABCD的形状（如图2），则四边形EFGH还是平行四边形吗？说明理由，参考小敏思考问题的方法解决一下问题；
2. （2）如图2，在（1）的条件下，若连接AC，BD.
  ①当AC与BD满足什么条件时，四边形EFGH是菱形，写出结论并证明；
  
  ②当AC与BD满足什么条件时，四边形EFGH是矩形，直接写出结论.
答案解析收藏纠错 + 选题
27. (2022八下·广陵期中) 在初中数学学习阶段，我们常常会利用一些变形技巧来简化式子，解答问题.
材料一：在解决某些分式问题时，倒数法是常用的变形技巧之一，所谓倒数法，即把式子变成其倒数形式，从而运用约分化简，以达到计算目的.

例：已知： $\text{[math]}$ ，求代数式x²+ $\text{[math]}$ 的值.

解：∵ $\text{[math]}$ ，∴ $\text{[math]}$ ＝4

即 $\text{[math]}$ ＝4∴x+ $\text{[math]}$ ＝4∴x²+ $\text{[math]}$ ＝（x+ $\text{[math]}$ ）²﹣2＝16﹣2＝14

材料二：在解决某些连等式问题时，通常可以引入参数“k”，将连等式变成几个值为k的等式，这样就可以通过适当变形解决问题.

例：若2x＝3y＝4z，且xyz≠0，求 $\text{[math]}$ 的值.

解：令2x＝3y＝4z＝k（k≠0）

则 $\text{[math]}$

根据材料回答问题：
1. （1）已知 $\text{[math]}$ ，求x+ $\text{[math]}$ 的值.
2. （2）已知 $\text{[math]}$ ，（abc≠0），求 $\text{[math]}$ 的值.
3. （3）若 $\text{[math]}$ ，x≠0，y≠0，z≠0，且abc＝7，求xyz的值.
答案解析收藏纠错 + 选题
28. (2022八下·广陵期中)
1. （1）【方法回顾】
  如图1，过正方形ABCD的顶点A作一条直线l交边BC于点P，BE⊥AP于点E，DF⊥AP于点F，若DF＝2.5，BE＝1，则EF＝．
2. （2）【问题解决】
  如图2，菱形ABCD的边长为1.5，过点A作一条直线l交边BC于点P，且∠DAP＝90°，点F是AP上一点，且∠BAD+∠AFD＝180°，过点B作BE⊥AB，与直线l交于点E，若EF＝1，求BE的长．
3. （3）【思维拓展】
  如图3，在正方形ABCD中，点P在AD所在直线上的上方，AP＝2，连接PB，PD，若△PAD的面积与△PAB的面积之差为m（m＞0），则PB²﹣PD²的值为．（用含m的式子表示）
答案解析收藏纠错 + 选题