
 B .
B .  C .
C .  D .
D . 

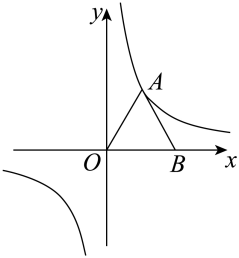
①将等边△ABO沿AO方向平移6个单位长度,恰好存在一个顶点在反比例函数的图象上;②将△ABO绕着点O分别逆时针旋转30°,60°,180°,210°,240°,恰好都存在一个顶点在反比例函数的图象上;③将等边△ABO以点O为位似中心,位似比为1,得到的位似图形恰好存在一个顶点在反比例函数的图象上;④将等边△ABO以直线或直线
为对称轴进行翻折,恰好存在一个顶点在反比例函数的图象上.
其中正确的是( )


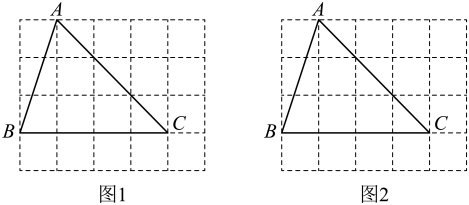
甲公司的方案:每月的养护费用y(元)与绿化面积x(平方米)的关系图象如图所示.
乙公司的方案:绿化面积不超过1000平方米时,每月收取费用5000元;绿化面积超过1000平方米时,超过的部分每月每平方米加收4元.

收集数据:
该市疫情防控部门的工作人员从郊区和城区部分市民中各抽取15名发放调查问卷,对疫情防控意识及常识性知识进行测试,测试成绩(百分制)如下:
郊区市民:74 81 75 76 70 75 75 79 81 70 74 80 91 69 82
城区市民:81 94 83 77 83 80 81 70 81 73 78 82 80 70 50
数据整理:
郊区市民 | 0 | 10 | 4 | 1 |
城区市民 | 1 | 8 | 1 |
说明:不低于90分为优秀;80~90分(含80分不含90分)为良好;60~80分(含60分不含80分)为及格;60分以下为不及格.
分析数据:
平均数 | 中位数 | 众数 | |
郊区市民 | 76.8 | 75 | |
城区市民 | 77.5 | 80 |
得出结论:
①在市中心某个居民区以家庭为单位随机抽取;
②在全市医务工作者中以家庭为单位随机抽取;
③在全市常住人口中以家庭为单位随机抽取.

①对称轴是直线;
②顶点坐标是;
③当时,y随x的增大而减小.
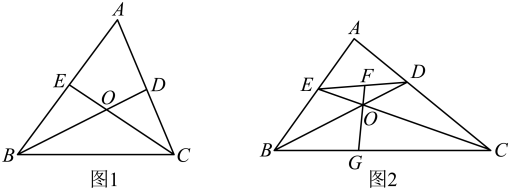
①求证:BC−BE−CD=2OF.
②延长FO交BC于点G,若OF=2,△DEO的面积为10,直接写出OG的长.