初中数学同步训练必刷题（北师大版七年级下册4. 5 利用三角...

更新时间：2023-03-18 浏览次数：121 类型：同步测试

一、单选题（每题3分，共30分）

1. (2023八上·日照月考)
如图所示，小明试卷上的三角形被墨迹污染了一部分，很快他就根据所学知识画出一个与试卷原图完全一样的三角形，那么两个三角形完全一样的依据是（　　）

A . ASA B . SAS C . AAS D . SSS

答案解析收藏纠错 + 选题
2. (2023八上·金乡县月考)
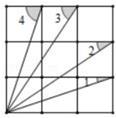
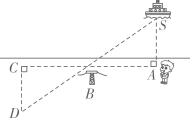
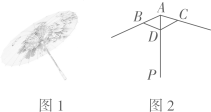
一块三角形玻璃样板不慎被小强同学碰破，成了四片完整四碎片（如图所示），聪明的小强经过仔细的考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板．你认为下列四个答案中考虑最全面的是（　　）

A . 带其中的任意两块去都可以 B . 带1、2或2、3去就可以了 C . 带1、4或3、4去就可以了 D . 带1、4或2、4或3、4去均可

答案解析收藏纠错 + 选题
3.
如图，小敏做了一个角平分仪ABCD，其中AB=AD，BC=DC，将仪器上的点与∠PRQ的顶点R重合，调整AB和AD，使它们分别落在角的两边上，过点A，C画一条射线AE，AE就是∠PRQ的平分线．此角平分仪的画图原理是：根据仪器结构，可得△ABC≌△ADC，这样就有∠QAE=∠PAE．则说明这两个三角形全等的依据是（　　）

A . SSS B . ASA C . AAS D . SAS

答案解析收藏纠错 + 选题
4.
要测量圆形工件的外径，工人师傅设计了如图所示的卡钳，点O为卡钳两柄交点，且有OA=OB=OC=OD，如果圆形工件恰好通过卡钳AB，则此工件的外径必是CD之长了，其中的依据是全等三角形的判定条件（　　）

A . SSS B . SAS C . ASA D . AAS

答案解析收藏纠错 + 选题
5. 要测量河两岸相对的两点A、B的距离，先在AB的垂线BF上取两点C、D，使CD=BC，再作出BF的垂线DE，使A、C、E在同一条直线上（如图），可以证明在△ABC≌△EDC，得ED=AB，因此，测得DE的长就是AB的长，在这里判定在△ABC≌△EDC的条件是（）

A . ASA B . SAS C . SSS D . HL

答案解析收藏纠错 + 选题
6. (2022七下·文登月考) 如图，红红书上的三角形被墨迹污染了一部分，她根据所学的知识很快就画了一个与书上完全一样的三角形，那么红红画图的依据是（）

A . SSS B . SAS C . ASA D . AAS

答案解析收藏纠错 + 选题
7. (2019八上·柳江期中) 如图，要测量河两岸相对的两点A、B的距离，先在AB的垂线BF上取两点C、D，使BC=CD，再作出BF的垂线DE，使点A、C、E在同一条直线上（如图所示），可以说明△ABC≌△EDC，得AB=DE，因此测得DE的长就是AB的长，判定△ABC≌△EDC，最恰当的理由是（）

A . 边角边 B . 角边角 C . 边边边 D . 边边角

答案解析收藏纠错 + 选题
8. 小明沿一段笔直的人行道行走，在由A步行到达B处的过程中，通过隔离带的空隙0点，刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语，其具体信息如下：如图，AB∥OE，OE∥CD，AC与BD相交于点O，OD⊥CD，垂足为点D，下列结论中不正确的是（）

A . ∠BOA=∠DOC B . AB∥CD C . ∠ABD=90° D . 与∠AOE相等的角共有2个

答案解析收藏纠错 + 选题
9. (2021七下·崂山期末) 在测量一个小口圆形容器的壁厚时，小明用“X型转动钳”按如图方法进行测量，其中OA＝OD，OB＝OC，测得AB＝a，EF＝b，圆形容器的壁厚是（）

A . a B . b C . b﹣a D . $\text{[math]}$ （b﹣a）

答案解析收藏纠错 + 选题
10.
如图，A在O的正北方向，B在O的正东方向，且A、B到点O的距离相等．甲从A出发，以每小时60千米的速度朝正东方向行驶，乙从B出发，以每小时40千米的速度朝正北方向行驶，1小时后，位于点O处的观察员发现甲、乙两人之间的夹角为45°，即∠COD=45°，此时甲、乙两人相距（　　）

A . 80千米 B . 50 $\text{[math]}$ 千米 C . 100千米 D . 100 $\text{[math]}$ 千米

答案解析收藏纠错 + 选题

二、填空题（每空3分，共24分）

11. (2022八上·新丰期中)
如图，小明书上的三角形被墨迹污染了一部分，他根据所学知识画出一个与此三角形全等的三角形，他画图依据的基本事实是

答案解析收藏纠错 + 选题
12.
野营活动中，小明用一张等腰三角形的铁皮代替锅，烙一块与铁皮形状、大小相同的饼，烙好一面后把饼翻身，这块饼能正好落在“锅”中．小丽有四张三角形的铁皮（如图所示），她想选择其中的一张铁皮代替锅，烙一块与所选铁皮形状、大小相同的饼，烙好一面后，将饼切一刀，然后将两小块都翻身，饼也能正好落在“锅”中．她的选择最多有种．

答案解析收藏纠错 + 选题
13. 用同样粗细、同种材料的金属线，制作两个全等的△ABC和△DEF．已知∠B=∠E，若AC边的质量为20千克，则DF边的质量为千克．

答案解析收藏纠错 + 选题
14.
如图，课间小明拿着老师的等腰三角板玩，不小心掉到两条凳子之间（凳子与地面垂直）．已知DC=a，CE=b．则两条凳子的高度之和为

答案解析收藏纠错 + 选题
15. (2021七上·济宁期末)
小明不慎将一块三角形的玻璃摔碎成如图所示的四块（即图中标有1、2、3、4的四块），你认为将其中的哪一块带去，就能配一块与原来一样大小的三角形？应该带第块．

答案解析收藏纠错 + 选题
16. (2024七下·深圳期中) 如图，是一个3×3的正方形网格，则∠1+∠2+∠3+∠4=。

答案解析收藏纠错 + 选题
17. (2022八上·仪征月考) 如图，小强站在河边的 $\text{[math]}$ 点处，在河的对面（小强的正北方向）的 $\text{[math]}$ 处有一电线塔，他想知道电线塔离他有多远，于是他向正西方向走了20步到达一棵树 $\text{[math]}$ 处，接着再向前走了20步到达 $\text{[math]}$ 处，然后他左转 $\text{[math]}$ 直行，当小强看到电线塔、树在一条直线时（即电线塔、树与自己现处的位置 $\text{[math]}$ 在一条直线上），他一共走了90步．如果小刚一步大约50厘米，估计小刚在点 $\text{[math]}$ 处时他与电线塔的距离为米．

答案解析收藏纠错 + 选题
18. (2020七下·南月考) 如图，小明与小敏玩跷跷板游戏，如果跷跷板的支点O（即跷跷板的中点）至地面的距离是50cm，当小敏从水平位置CD下降40cm时，这时小明离地面的高度是．

答案解析收藏纠错 + 选题

三、解答题（共7题，共66分）

19. (2023八上·张店月考) 如图是一个工业开发区局部的设计图，河的同一侧有两个工厂A和B，AD、BC的长表示两个工厂到河岸的距离，其中E是进水口，D、C为两个排污口．已知AE＝BE，∠AEB＝90°，AD⊥DC，BC⊥DC，点D、E、C在同一直线上，AD＝150米，BC＝350米，求两个排污口之间的水平距离DC．

答案解析收藏纠错 + 选题
20. (2022七下·榆阳期末) 如图，小明站在堤岸的A点处，正对他的S点停有一艘游艇.他想知道这艘游艇距离他有多远，于是他沿堤岸走到电线杆B旁，接着沿 $\text{[math]}$ 再往前走相同的距离，到达C点（即 $\text{[math]}$ ），然后他向左直行，当看到电线杆与游艇在一条直线上时停下来，此时他位于D点（在小明从A走到D的过程中，游艇未移动）.小明测得C、D两点间的距离为 $\text{[math]}$ ，求在A点处小明与游艇的距离 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
21. (2022七下·榆林期末) 如图是一张简易木床的侧面图，现要钉上两根木条以确保其坚固耐用，木条 $\text{[math]}$ 已经钉上了 $\text{[math]}$ ，如果为了美观，要求木条 $\text{[math]}$ 与木条 $\text{[math]}$ 等长，那么应该怎样确定点 $\text{[math]}$ 的位置?并说明理由.

答案解析收藏纠错 + 选题
22. (2023七下·凤翔期末) 如图1，油纸伞是中国传统工艺品之一，起源于中国的一种纸制或布制伞．油纸伞的制作工艺十分巧妙，如图2，伞圈D沿着伞柄AP滑动时，总有伞骨 $\text{[math]}$ ， $\text{[math]}$ ，从而使得伞柄AP始终平分同一平面内两条伞骨所成的 $\text{[math]}$ ．请你说明其中的理由．

答案解析收藏纠错 + 选题
23. (2022七下·武功期末) 如图，小明和小华住在同一个小区不同单元楼，他们想要测量小明家所在单元楼AB的高度，首先他们在两栋单元楼之间选定一点E，然后小华在自己家阳台C处测得E处的俯角为∠1，小明站在E处测得楼顶A的仰角为∠2，发现∠1与∠2互余，过点F作FG⊥AB于点G，已知BG＝1米，BE＝CD＝20米，BD＝58米，点B、E、D在一条直线上，AB⊥BD，FE⊥BD，CD⊥BD，试求单元楼AB的高．（注：BE＝FG，BG＝EF，∠1与∠3互余）

答案解析收藏纠错 + 选题
24. 如图，点B，F，C，E在直线l上（点F，点C之间不能直接测量），点A，D在l异侧，测得AB=DE，AC=DF，BF=EC．
1. （1）求证：△ABC≌△DEF；
2. （2）指出图中所有平行的线段，并说明理由．
答案解析收藏纠错 + 选题
25. (2021七下·青山期末) 某校七年级学生到野外活动，为测量一池塘两端A ， B的距离，甲、乙、丙三位同学分别设计出如下几种方案：

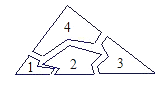
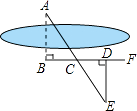
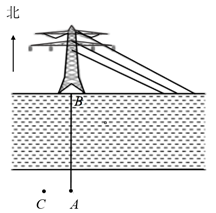
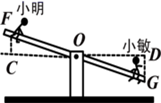
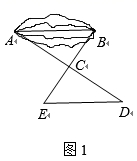
甲：如图①，先在平地取一个可直接到达A ， B的点C ，再连接AC ， BC ，并分别延长AC至D ， BC至E ，使DC＝AC ， EC＝BC ，最后测出DE的长即为A ， B的距离．

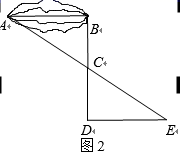
乙：如图②，先过点B作AB的垂线，再在垂线上取C ， D两点，使BC＝CD ，接着过点D作BD的垂线DE ，交AC的延长线于点E ，则测出DE的长即为A ， B的距离．

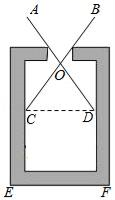
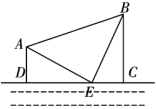
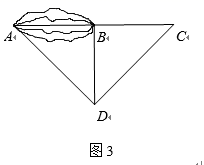
丙：如图③，过点B作BD⊥AB ，再由点D观测，在AB的延长线上取一点C ，使∠BDC＝∠BDA ，这时只要测出BC的长即为A ， B的距离．
1. （1）以上三位同学所设计的方案，可行的有；
2. （2）请你选择一可行的方案，说说它可行的理由．
答案解析收藏纠错 + 选题