
成绩/分 | 86 | 88 | 90 | 92 | 94 | 95 | 96 | 98 | 100 |
人数 | ■ | 1 | ■ | 1 | 4 | 5 | 6 | 5 | 15 |
下列关于成绩的统计量中,与被遮盖的数据有关的是( )
一分钟跳绳成绩的分组统计表
组别 | 跳绳次数分段 | 频数 |
A | 10 | |
B | ||
C | 42 | |
D | 13 |
一分钟跳绳成绩的扇形统计图

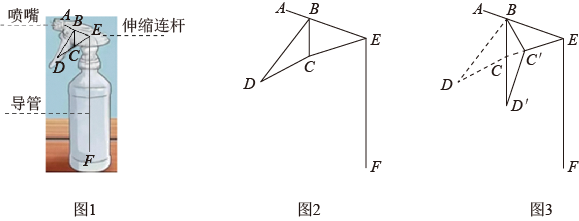
①以点为坐标原点,
所在的直线为
轴建立平面直角坐标系;
②在平面直角坐标系中,绘制反比例函数的图象,图象与
的边
交于点
;
③以点为圆心,
为半径作弧,交函数
的图象于点
;
④分别过点和
作
轴和
轴的平行线,两线交于点
,
;
⑤作射线 , 交
于点
, 得到
.


