广东省深圳市福田区2023年九年级3月质量检测数学试题

更新时间：2023-04-27 浏览次数：106 类型：中考模拟

一、单选题

1. (2023·福田模拟) 下列四个选项中，为负整数的是（）

A . 0 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023·福田模拟) 下列图形中，是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2023·福田模拟) 2022年深圳全市地区生产总值3.24万亿元.3.24万亿用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023·福田模拟) 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023·福田模拟) 如图，一个含有 $\text{[math]}$ 角的直角三角尺的两个顶点放在直尺的对边上．如果 $\text{[math]}$ ，那么 $\text{[math]}$ 的度数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024九下·凉州模拟) 一件商品售价 $\text{[math]}$ 元，利润率为 $\text{[math]}$ ，则这种商品每件的成本是（）元．

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023·宝安模拟) 如图，甲乙两楼相距30米，乙楼高度为36米，自甲楼顶A处看乙楼楼顶B处仰角为 $\text{[math]}$ ，则甲楼高度为（）

A . 15米 B . $\text{[math]}$ 米 C . $\text{[math]}$ 米 D . $\text{[math]}$ 米

答案解析收藏纠错 + 选题
8. (2023·宝安模拟) 下列说法正确的是（）

A . 对角线互相垂直的四边形是菱形 B . 对应边成比例的四边形是相似四边形 C . 二次函数 $\text{[math]}$ （ $\text{[math]}$ 为常数）的图象与 $\text{[math]}$ 轴有两个交点 D . 若代数式 $\text{[math]}$ 在实数范围内有意义，则 $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2023·宝安模拟) 我们定义一种新函数：形如 $\text{[math]}$ 的函数叫做“鹊桥”函数．数学兴趣小组画出一个“鹊桥”函数 $\text{[math]}$ 的图像如图所示，则下列结论正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 当直线 $\text{[math]}$ 与该图像恰有三个公共点时，则 $\text{[math]}$ D . 关于 $\text{[math]}$ 的方程 $\text{[math]}$ 的所有实数根的和为4

答案解析收藏纠错 + 选题
10. (2023·福田模拟) 如图，四边形 $\text{[math]}$ 和四边形 $\text{[math]}$ 均为正方形，点 $\text{[math]}$ 为 $\text{[math]}$ 的中点，若 $\text{[math]}$ ，连接 $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2024九下·顺义月考) 分解因式： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
12. (2023·福田模拟) 宝鸡“我要上全运”马拉松赛事设有A“全程马拉松”，B“半程马拉松”，C：“嘉年华马拉松”三个项目，小智和小慧参加了该赛事的志愿者服务工作，组委会将志愿者随机分配到三个项目组.小智和小慧被分到同一个项目组进行志愿服务的概率.

答案解析收藏纠错 + 选题
13. (2023·福田模拟) 如图所示，在 $\text{[math]}$ 中， $\text{[math]}$ ，按以下步骤作图：①以点 $\text{[math]}$ 为圆心，以小于 $\text{[math]}$ 的长为半径作弧，分别交 $\text{[math]}$ 、 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ；②分别以点 $\text{[math]}$ ， $\text{[math]}$ 为圆心，以大于 $\text{[math]}$ 的长为半径作弧，两弧相交于点 $\text{[math]}$ ；③作射线 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ．则 $\text{[math]}$ 的长为．

答案解析收藏纠错 + 选题
14. (2023·福田模拟) 如图，反比例函数 $\text{[math]}$ 的图象经过点 $\text{[math]}$ ，将线段 $\text{[math]}$ 沿 $\text{[math]}$ 轴向右平移至 $\text{[math]}$ ，反比例函数 $\text{[math]}$ 的图象经过点 $\text{[math]}$ ．若线段 $\text{[math]}$ 扫过的面积为 $\text{[math]}$ ，则 $\text{[math]}$ 的值为

答案解析收藏纠错 + 选题
15. (2024·浙江模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 在边 $\text{[math]}$ 上， $\text{[math]}$ ，将 $\text{[math]}$ 沿 $\text{[math]}$ 折叠， $\text{[math]}$ 的对应边 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长为

答案解析收藏纠错 + 选题

三、解答题

16. (2023九下·长沙模拟) 计算： $\text{[math]}$

答案解析收藏纠错 + 选题
17. (2023·福田模拟) 先化简: $\text{[math]}$ ，并在 $\text{[math]}$ 中选一个合适的数求值.

答案解析收藏纠错 + 选题
18. (2023·福田模拟) 为了解学生的睡眠情况，某校随机抽取部分学生对他们最近两周的睡眠情况进行调查，得到他们每日平均睡眠时长x（单位：h）的一组数据，将所得数据分为四组（A：x＜8；B：8≤x＜9；C：9≤x＜10；D：x≥10），并绘制成如下两幅不完整的统计图．
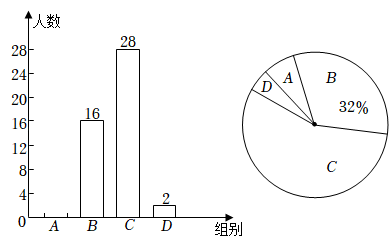
根据以上信息，解答下列问题：
1. （1）本次一共抽样调查了名学生．
2. （2）求出扇形统计图中D组所对应的扇形圆心角的度数．
3. （3）将条形统计图补充完整．
4. （4）若该校共有1200名学生，请估计最近两周有多少名学生的每日平均睡眠时长大于或等于9h．
答案解析收藏纠错 + 选题
19. (2023九上·龙岗月考) 某企业计划购买A、 $\text{[math]}$ 两种型号的机器人来搬运货物，已知每台A型机器人比每台 $\text{[math]}$ 型机器人每天少搬运10吨，且A型机器人每天搬运540吨货物与 $\text{[math]}$ 型机器人每天搬运600吨货物所需台数相同．
1. （1）求每台A型机器人和每台 $\text{[math]}$ 型机器人每天分别搬运货物多少吨？
2. （2）每台A型机器人售价1.2万元，每台 $\text{[math]}$ 型机器人售价2万元，该公司计划采购A、 $\text{[math]}$ 两种型号的机器人共30台，必须满足每天搬运的货物不低于2830吨，购买金额不超过48万元．请你求出最节省的采购方案，购买总金额最低是多少万元？
答案解析收藏纠错 + 选题
20. (2023·宝安模拟) 如图， $\text{[math]}$ 为 $\text{[math]}$ 的直径，点 $\text{[math]}$ 在直径 $\text{[math]}$ 上（点 $\text{[math]}$ 与A， $\text{[math]}$ 两点不重合）， $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 上满足 $\text{[math]}$ ，连接 $\text{[math]}$ 并延长到 $\text{[math]}$ 点，使 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ 是 $\text{[math]}$ 的切线；
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
21. (2023·福田模拟) 【综合实践】
某公园在人工湖里安装一个喷泉，在湖心处竖直安装一根水管，在水管的顶端安一个喷水头，喷出的水柱形状可以看作是抛物线的一部分．若记水柱上某一位置与水管的水平距离为 $\text{[math]}$ 米，与湖面的垂直高度为 $\text{[math]}$ 米．下面的表中记录了 $\text{[math]}$ 与 $\text{[math]}$ 的五组数据：
$\text{[math]}$ （米）
0
1
2
3
4
$\text{[math]}$ （米）
0.5
1.25
1.5
1.25
0.5
1. （1）在下面网格（图1）中建立适当的平面直角坐标系，并根据表中所给数据画出表示 $\text{[math]}$ 与 $\text{[math]}$ 函数关系的图象；
2. （2）若水柱最高点距离湖面的高度为 $\text{[math]}$ 米，则 $\text{[math]}$ ▲ ，并求 $\text{[math]}$ 与 $\text{[math]}$ 函数表达式；
3. （3）现公园想通过喷泉设立新的游玩项目，准备通过只调节水管露出湖面的高度，使得游船能从抛物线形水柱下方通过，如图2所示，为避免游船被喷泉淋到，要求游船从抛物线形水柱下方中间通过时，顶棚上任意一点到水柱的竖直距离均不小于0.5米，已知游船顶棚宽度为3米，顶棚到湖面的高度为2米，那么公园应将水管露出湖面的高度（喷水头忽略不计）至少调节到多少米才能符合要求？请通过计算说明理由（结果保留一位小数）．
答案解析收藏纠错 + 选题
22. (2023·福田模拟)
1. （1）【问题初探】
  如图1，等腰 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 边一点，以 $\text{[math]}$ 为腰向下作等腰 $\text{[math]}$ ， $\text{[math]}$ ．连接 $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 的中点，连接 $\text{[math]}$ ．猜想并证明线段 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系和位置关系．
2. （2）【深入探究】
  在（1）的条件下，如图2，将等腰 $\text{[math]}$ 绕点 $\text{[math]}$ 旋转，上述结论是否仍然成立？若成立，请证明；若不成立，请说明理由．
3. （3）【拓展迁移】
  如图3，等腰 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ．在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ．连接 $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 的中点，连接 $\text{[math]}$ ．
  $\text{[math]}$ 绕点 $\text{[math]}$ 旋转过程中，
  ①线段 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系为：；
  ②若 $\text{[math]}$ ， $\text{[math]}$ ，当点 $\text{[math]}$ 在等腰 $\text{[math]}$ 内部且 $\text{[math]}$ 的度数最大时，线段 $\text{[math]}$ 的长度为．
答案解析收藏纠错 + 选题