| 年龄(岁) | 14 | 15 | 16 | 17 | 18 |
| 人数(人) | 1 | 4 | 3 | 2 | 2 |


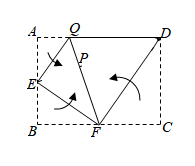



①若 , 求
之间的数量关系.
②若 , 求
的最小值.
①求与x之间的函数关系式.
②写出该函数的两条性质.
①若关于x的方程x2-4x-m=0有解,求m的取值范围.小明思考过程如下:由x2-4x-m=0得m=x2-4x,m是关于x的二次函数,根据x的范围可以求出m的取值范围.请你完成解题过程.
②若关于x的方程有解,请直接写出m的取值范围.
②如图3,当四边形的顶点
落在直线
上时,求
的面积;