6.
(2023·安徽模拟)
巴普士(约公元3~4世纪),古希腊亚历山大学派著名几何学家.生前有大量的著作,但大部分遗失在历史长河中,仅有《数学汇编》保存下来.《数学汇编》一共8卷,在《数学汇编》第3卷中记载着这样一个定理:“如果在同一平面内的一个闭合图形的内部与一条直线不相交,那么该闭合图形围绕这条直线旋转一周所得到的旋转体的体积等于该闭合图形的面积与该闭合图形的重心旋转所得周长的积”,

(

表示平面闭合图形绕旋转轴旋转所得几何体的体积,S表示闭合图形的面积,l表示重心绕旋转轴旋转一周的周长).已知在梯形ABCD中,

,

,

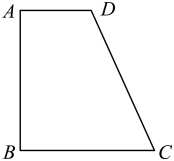
, 利用上述定理可求得梯形ABCD的重心G到点B的距离为( )