题库组卷系统-专注K12在线组卷服务

在线咨询

当前：高中数学

当前位置：高中数学 /高考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

上海市奉贤区2023届高三数学二模试卷

更新时间：2023-05-18 浏览次数：63 类型：高考模拟

一、填空题

1. (2023高三上·静安月考) 已知集合 $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
2. (2023高三上·静安月考) 已知 $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ 是虚数单位，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
3. (2023·奉贤模拟) 在 $\text{[math]}$ 的展开式中， $\text{[math]}$ 的系数为.（用数字作答）

答案解析收藏纠错 + 选题
4. (2023高三上·静安月考) 已知圆柱的上、下底面的中心分别为 $\text{[math]}$ 、 $\text{[math]}$ ，过直线 $\text{[math]}$ 的平面截该圆柱所得的截面是面积为8的正方形，则该圆柱的侧面积为．

答案解析收藏纠错 + 选题
5. (2023·奉贤模拟) 2017年5月某校高三年级1600名学生参加了教育局组织的期末统考，已知数学考试成绩 $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ .（试卷满分为150分）统计结果显示数学考试成绩在80分到120分之间的人数约为总人数的 $\text{[math]}$ ，则此次统考中成绩不低于120分的学生人数约为.

答案解析收藏纠错 + 选题
6. (2023高三上·静安月考) 已知两个正数 $\text{[math]}$ ， $\text{[math]}$ 的几何平均值为1，则 $\text{[math]}$ 的最小值为．

答案解析收藏纠错 + 选题
7. (2023·奉贤模拟) 某种动物从出生起活到20岁的概率为0.8，从出生起活到25岁的概率为0.4，现有一个20岁的这种动物，它能活到25岁的概率为.

答案解析收藏纠错 + 选题
8. (2023·奉贤模拟) 已知随机变量 $\text{[math]}$ 的分布为 $\text{[math]}$ ，且 $\text{[math]}$ ，若 $\text{[math]}$ ，则实数 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
9. (2023·奉贤模拟) 设圆 $\text{[math]}$ 与双曲线 $\text{[math]}$ 的一条渐近线相切，则该双曲线的渐近线方程为．

答案解析收藏纠错 + 选题
10. (2023·奉贤模拟) $\text{[math]}$ 内角 $\text{[math]}$ 的对边分别为 $\text{[math]}$ ，若 $\text{[math]}$ 的面积为 $\text{[math]}$ ，则 $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2023·奉贤模拟) 在集合 $\text{[math]}$ 中任取一个偶数 $\text{[math]}$ 和一个奇数 $\text{[math]}$ 构成一个以原点为起点的向量 $\text{[math]}$ ，从所有得到的以原点为起点的向量中任取两个向量为邻边作平行四边形，面积不超过4的平行四边形的个数是．

答案解析收藏纠错 + 选题
12. (2023高三上·静安月考) 已知 $\text{[math]}$ 为 $\text{[math]}$ 上的奇函数，且当 $\text{[math]}$ 时， $\text{[math]}$ ，则 $\text{[math]}$ 的驻点为．

答案解析收藏纠错 + 选题

二、单选题

13. (2023·奉贤模拟) “ $\text{[math]}$ ”是“直线 $\text{[math]}$ 与 $\text{[math]}$ 垂直”的

A . 充分不必要条件 B . 必要不充分条件 C . 充要条件 D . 既不充分也不必要条件

答案解析收藏纠错 + 选题
14. (2023·奉贤模拟) 下列函数中，以 $\text{[math]}$ 为周期且在区间 $\text{[math]}$ 单调递增的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
15. (2023·奉贤模拟) 某校一个课外学习小组为研究某作物种子的发芽率y和温度x（单位：℃）的关系，在20个不同的温度条件下进行种子发芽实验，由实验数据 $\text{[math]}$ 得到下面的散点图：

由此散点图，在10℃至40℃之间，下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
16. (2023·奉贤模拟) 设 $\text{[math]}$ 是一个无穷数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和，若一个数列满足对任意的正整数 $\text{[math]}$ ，不等式 $\text{[math]}$ 恒成立，则称数列 $\text{[math]}$ 为和谐数列，有下列3个命题：
①若对任意的正整数 $\text{[math]}$ 均有 $\text{[math]}$ ，则 $\text{[math]}$ 为和谐数列；
②若等差数列 $\text{[math]}$ 是和谐数列，则 $\text{[math]}$ 一定存在最小值；
③若 $\text{[math]}$ 的首项小于零，则一定存在公比为负数的一个等比数列是和谐数列．
以上3个命题中真命题的个数有（）个

A . 0 B . 1 C . 2 D . 3

答案解析收藏纠错 + 选题

三、解答题

17. (2023·奉贤模拟) 已知等差数列 $\text{[math]}$ 的公差不为零， $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 成等比数列．
1. （1）求 $\text{[math]}$ 的通项公式；
2. （2）计算 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
18. (2023·奉贤模拟) 如图，在四棱锥 $\text{[math]}$ 中， $\text{[math]}$ ，且 $\text{[math]}$ ．
1. （1）证明：平面 $\text{[math]}$ 平面 $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，且四棱锥 $\text{[math]}$ 的体积为 $\text{[math]}$ ，求 $\text{[math]}$ 与平面 $\text{[math]}$ 所成的线面角的大小．
答案解析收藏纠错 + 选题
19. (2023·奉贤模拟) 设函数 $\text{[math]}$ 的定义域是R，它的导数是 $\text{[math]}$ ．若存在常数 $\text{[math]}$ $\text{[math]}$ ，使得 $\text{[math]}$ 对一切 $\text{[math]}$ 恒成立，那么称函数 $\text{[math]}$ 具有性质 $\text{[math]}$ ．
1. （1）求证：函数 $\text{[math]}$ 不具有性质 $\text{[math]}$ ；
2. （2）判别函数 $\text{[math]}$ 是否具有性质 $\text{[math]}$ ．若具有求出 $\text{[math]}$ 的取值集合；若不具有请说明理由．
答案解析收藏纠错 + 选题
20. (2023·奉贤模拟) 某小区有块绿地，绿地的平面图大致如下图所示，并铺设了部分人行通道．
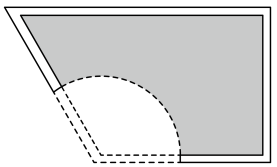
为了简单起见，现作如下假设：
假设1：绿地是由线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 和弧 $\text{[math]}$ 围成的，其中 $\text{[math]}$ 是以 $\text{[math]}$ 点为圆心，圆心角为 $\text{[math]}$ 的扇形的弧，见图1；
假设2：线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 所在的路行人是可通行的，圆弧 $\text{[math]}$ 暂时未修路；
假设3：路的宽度在这里暂时不考虑；
假设4：路用线段或圆弧表示，休息亭用点表示．
图1-图3中的相关边、角满足以下条件：
直线 $\text{[math]}$ 与 $\text{[math]}$ 的交点是 $\text{[math]}$ ， $\text{[math]}$ $\text{[math]}$ ， $\text{[math]}$ ． $\text{[math]}$ 米．
小区物业根据居民需求，决定在绿地修建一个休息亭．根据不同的设计方案解决相应问题，结果精确到米．
1. （1）假设休息亭建在弧 $\text{[math]}$ 的中点，记为 $\text{[math]}$ ，沿 $\text{[math]}$ 和线段 $\text{[math]}$ 修路，如图2所示．求 $\text{[math]}$ 的长；
2. （2）假设休息亭建在弧 $\text{[math]}$ 上的某个位置，记为 $\text{[math]}$ ，作 $\text{[math]}$ 交 $\text{[math]}$ 于 $\text{[math]}$ ，作 $\text{[math]}$ 交 $\text{[math]}$ 于 $\text{[math]}$ ．沿 $\text{[math]}$ 、线段 $\text{[math]}$ 和线段 $\text{[math]}$ 修路，如图3所示．求修建的总路长 $\text{[math]}$ 的最小值；
3. （3）请你对（1）和（2）涉及到的两种设计方案做个简明扼要的评价．
答案解析收藏纠错 + 选题
21. (2023·奉贤模拟) 已知椭圆 $\text{[math]}$ ： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．椭圆 $\text{[math]}$ 内部的一点 $\text{[math]}$ $\text{[math]}$ ，过点 $\text{[math]}$ 作直线 $\text{[math]}$ 交椭圆于 $\text{[math]}$ ，作直线 $\text{[math]}$ 交椭圆于 $\text{[math]}$ ． $\text{[math]}$ 、 $\text{[math]}$ 是不同的两点．
1. （1）若椭圆 $\text{[math]}$ 的离心率是 $\text{[math]}$ ，求 $\text{[math]}$ 的值；
2. （2）设 $\text{[math]}$ 的面积是 $\text{[math]}$ ， $\text{[math]}$ 的面积是 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ 时，求 $\text{[math]}$ 的值；
3. （3）若点 $\text{[math]}$ ， $\text{[math]}$ 满足 $\text{[math]}$ 且 $\text{[math]}$ ，则称点 $\text{[math]}$ 在点 $\text{[math]}$ 的左上方．求证：当 $\text{[math]}$ 时，点 $\text{[math]}$ 在点 $\text{[math]}$ 的左上方．
答案解析收藏纠错 + 选题

试卷信息