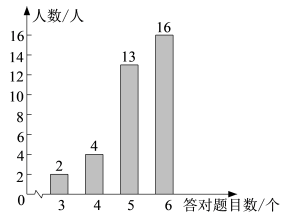



根据统计图提供的信息,有下列三个结论:
①按日接待游客数从高到低排名,2月6日在这14天中排名第4;
②记第一周,第二周日接待游客数的方差分别为s12 , s22 , 则s12>s22;
③这14天日接待游客数的众数和中位数都是2.0千人.
其中所有正确结论的序号是.
已知:▱ABCD.
求作:点P,使点P为边AB的中点.
作法:
①作射线DA;
②以点A为圆心,BC长为半径画弧,
在点A左侧与射线DA交于点E;
③连接CE交AB于点P.
点P即为所求作的边AB的中点.
根据小芸设计的尺规作图过程,

证明:连接AC,EB,
∵四边形ABCD是平行四边形,
∴AE∥BC.
∵AE= ▲ ,
∴四边形EBCA是平行四边形,( )(填推理的依据)
∴AP=PB,( )(填推理的依据)
点P即为所求作的边AB的中点.


x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 5 | 4 | m | 2 | 1 | 0 | 1 | 2 | 3 | … |
其中,m=;

当x<2时,y随x的增大而减小;当x≥2时,y随x的增大而;
①不等式|x-2|≥1.5的解集是;
②若关于x的方程|x-2|=kx (k≠0)只有一个解,则k的取值范围是.
a.八年级课后延时服务家长评分数据的频数分布表如下(数据分为5组:0≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100):
分组 | 频数 |
0≤x<60 | 2 |
60≤x<70 | 5 |
70≤x<80 | 15 |
80≤x<90 | a |
90≤x≤100 | 8 |
合计 | 50 |
b.八年级课后延时服务家长评分在80≤x<90这一组的数据按从小到大的顺序排列,前5个数据如下:
81,81,82,83,83.
c.七,八年级课后延时服务家长评分的平均数,中位数,众数如下表:
年级 | 平均数 | 中位数 | 众数 |
七 | 78 | 79 | 85 |
八 | 81 | b | 83 |
根据以上信息,回答下列问题:

若在y轴上存在点N,使得∠MNP=90°,且NM=NP,则称点P为m直角等腰点.例如,点P(-2,0)为2直角等腰点,理由如下:如图,设M(2,0),以MP为斜边作等腰直角△PMN,可得y轴上的一个点N(0,2),所以点P(-2,0)为2直角等腰点.
