次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
成绩/米 | 9.7 | 9.6 | 9.8 | 10 | 9.8 | 9.9 | 10.1 |
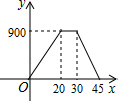 B .
B . 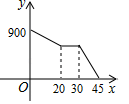 C .
C . 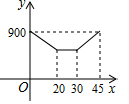 D .
D . 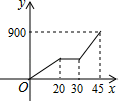

 B .
B .  C .
C .  D .
D . 

航天技术 | 生物技术 | 能源技术 | 其它技术领域 | |
小亮 | 85 | 90 | 95 | 90 |
小明 | 100 | 90 | 80 | 90 |
若“航天技术”,“生物技术”,“能源技术”,“其它技术领域”四个项目按确定综合成绩,则小亮和小明谁的综合成绩高?请通过计算说明理由.

名称 | A种西瓜 | B种西瓜 |
进价(元/千克) | 4 | 3 |
售价(元/千克) | 6 | 4 |
设A种西瓜批发x千克,全部售完后总利润为y元.
运用“双求法”证明勾股定理勾股定理表现了我国古人对数学的钻研精神和聪明才智,是我国古代数学的骄傲,它神秘而美妙,证法多样,是数学定理中证明方法最多的定理之一.勾股定理的证明过程多数采用的方法是“用两种不同的方法和含有a,b,c的式子表示同一个图形的面积”,由于同一个图形的面积相等,从而得到含a,b,c的恒等式,通过化简即可完成勾股定理的证明.数学上把这种方法称之为“双求法”. 下面是利用“双求法”证明勾股定理的一种思路: 如图1,将两个全等的直角三角形
|
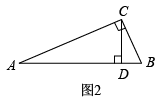
如图2,中,
, CD是AB边上的高,若
,
, 则
.(直接写出答案)
问题情境:学习完平行四边形的性质和判定后,老师创设了如下探究情境,探究三角形的中位线定理.
问题1:如图1,在中,对角线AC,BD相交于点O,E为AB上一点,连接EO并延长交CD于F,则OE与OF有怎样的数量关系?

小明: .
理由如下:∵四边形ABCD是平行四边形,
∴ ,
(依据1)
∴
又∵ ,
∴(依据2).
∴
问题2:如图2,若点E为AB的中点,其他条件不变,则线段EF与BC有怎样的数量关系和位置关系?
小亮: ,
BC.
理由如下:….
问题3:如图3,在中,D,E分别是AB,AC的中点,连接DE,像DE这样,连接三角形两边中点的线段叫做三角形的中位线.通过前面问题给你的启发,你能猜想出DE和BC的数量关系和位置关系吗?
小慧:BC,
.
…
数学思考:
依据1:;依据2:.
请用图3写出三角形中位线定理的证明过程.
①请用含m的式子表示出S;
②当的面积等于
面积的
时,求出m的值;