山东省济南市2023年中考二模数学试题

更新时间：2024-07-13 浏览次数：110 类型：中考模拟

一、单选题

1. (2023·济南模拟) 如图所示三视图的几何体是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2023七下·中江月考) $\text{[math]}$ 的相反数为 $\text{[math]}$ 　　 $\text{[math]}$

A . $\text{[math]}$ B . 3 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024九下·天桥模拟) 地球绕太阳转动一天通过的路程约是2640000千米，用科学记数法表示为（）

A . 2.64×10⁷ B . 2.64×10⁶ C . 26.4×10⁵ D . 264×10⁴

答案解析收藏纠错 + 选题
4. (2023·济南模拟) 加强生活垃圾管理，维护公共环境和节约资源是全社会公共的责任.我市将全面推行生活垃圾强制分类.下列四个垃圾分类标识中的图形是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2023·济南模拟) 已知实数a，b在数轴上的对应点的位置如图所示，下列结论正确的是（）

A . a﹣b＞0 B . a+b＞0 C . ab＞0 D . |a+1|＜|b+1|

答案解析收藏纠错 + 选题
6. (2023·济南模拟) 如图， $\text{[math]}$ ∥ $\text{[math]}$ ， $\text{[math]}$ 为直线 $\text{[math]}$ 上两点，且 $\text{[math]}$ 平分 $\text{[math]}$ ；若 $\text{[math]}$ ，则∠2的度数为（　　　）

A . 30° B . 36° C . 42° D . 45°

答案解析收藏纠错 + 选题
7. (2023·济南模拟) 如图，电路图上有四个开关 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 和一个小灯泡，闭合开关 $\text{[math]}$ 或同时闭合开关 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 都可使小灯泡发光，则任意闭合其中两个开关，小灯泡发光的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023·济南模拟) 某大桥采用了低塔斜拉桥桥型（如图1），图2是从图1抽象出的平面图，假设站在桥上测得拉索 $\text{[math]}$ 与水平桥面的夹角是30°，拉索 $\text{[math]}$ 的坡度（或坡比） $\text{[math]}$ ，两拉索底端距离 $\text{[math]}$ 是18米，则立柱 $\text{[math]}$ 的高度是（）

A . 18米 B . $\text{[math]}$ 米 C . $\text{[math]}$ 米 D . 9米

答案解析收藏纠错 + 选题
9. (2024八上·福田期末) 如图，在 $\text{[math]}$ 中，AB＝AC，分别以点A、B为圆心，以适当的长为半径作弧，两弧分别交于E，F，作直线EF，D为BC的中点，M为直线EF上任意一点.若BC＝4， $\text{[math]}$ 面积为10，则BM+MD长度的最小值为（）

A . $\text{[math]}$ B . 3 C . 4 D . 5

答案解析收藏纠错 + 选题
10. (2023·济南模拟) 规定：在平面直角坐标系中，横坐标与纵坐标均为整数的点为整点．对于题目：抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴分别交于 $\text{[math]}$ 、 $\text{[math]}$ 两点（点M在点N的左侧）， $\text{[math]}$ ，线段 $\text{[math]}$ 与抛物线围成的封闭区域记作 $\text{[math]}$ （包括边界），若区域 $\text{[math]}$ 内有6个整点，求 $\text{[math]}$ 的取值范围．则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ 或 $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2023·济南模拟) 在实数范围内分解因式： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
12. (2023·济南模拟) 在卡塔尔世界杯上，来自中国制造的主体育场馆“大金碗”——卢塞尔体育场（图①），融合了许多黑科技，球场顶棚采用环保膜材料，既可以为观众提供遮阳，又能够给球场草地带来阳光．膜的材料结构是由许多正六边形交织而成的，正六边形 $\text{[math]}$ （图②）中， $\text{[math]}$ 为°．

答案解析收藏纠错 + 选题
13. (2023·济南模拟) 某学习小组在“世界读书日”这天统计了本组5名同学在上学期阅读课外书籍的册数，数据是18，x，15，16，13，若这组数据的平均数为16，则这组数据的中位数是．

答案解析收藏纠错 + 选题
14. (2023·济南模拟) 分式方程 $\text{[math]}$ 的解为x＝．

答案解析收藏纠错 + 选题
15. (2024九上·广东期末) 如图，正方形的顶点 $\text{[math]}$ 分别在 $\text{[math]}$ 轴和 $\text{[math]}$ 轴上，边 $\text{[math]}$ 的中点 $\text{[math]}$ 在 $\text{[math]}$ 轴上，若反比例函数 $\text{[math]}$ 的图象恰好经过 $\text{[math]}$ 的中点 $\text{[math]}$ ，则 $\text{[math]}$ 的长为．

答案解析收藏纠错 + 选题
16. (2023·济南模拟) 如图，在矩形纸片ABCD中，AD＝10，AB＝8，将AB沿AE翻折，使点B落在 $\text{[math]}$ 处，AE为折痕；再将EC沿EF翻折，使点C恰好落在线段EB'上的点 $\text{[math]}$ 处，EF为折痕，连接 $\text{[math]}$ .若CF＝3，则tan $\text{[math]}$ ＝.

答案解析收藏纠错 + 选题

三、解答题

17. (2024九下·日照月考) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
18. (2023·济南模拟) 解不等式组： $\text{[math]}$ ，并写出 $\text{[math]}$ 的所有整数解．

答案解析收藏纠错 + 选题
19. (2023八下·宁远期中) 已知：如图，在平行四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 是对角线 $\text{[math]}$ 上两点，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 求证： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
20. (2023·济南模拟) 某校政治实践小组就近期人们比较关注的五个话题：“A.5G通讯；B．民法典；C．北斗导航；D．数字经济；E ．小康社会”，对学生进行了随机抽样调查，每人只能从中选择一个本人最关注的话题，根据调查结果绘制了如图两幅不完整的统计图．
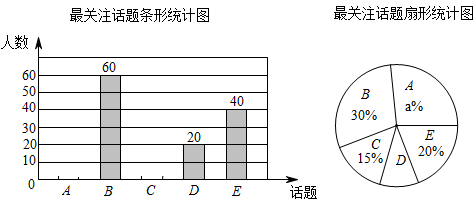
请结合统计图中的信息，解决下列问题：
1. （1）政治实践小组在这次活动中，调查的学生共有人；
2. （2）将图中的最关注话题条形统计图补充完整；
3. （3）政治实践小组进行专题讨论中，甲、乙两个小组从三个话题：“A.5G通讯；B．民法典；C．北斗导航”中抽签（不放回）选一项进行发言，利用树状图或表格，求出两个小组选择A、B话题发言的概率．
答案解析收藏纠错 + 选题
21. (2023·济南模拟) 如图，在数学综合实践活动课上，两名同学要测量小河对岸大树BC的高度，甲同学在点A测得大树顶端B的仰角为45°，乙同学从A点出发沿斜坡走6 $\text{[math]}$ 米到达斜坡上点D，在此处测得树顶端点B的仰角为26.7°，且斜坡AF的坡度为1：2．
1. （1）求乙同学从点A到点D的过程中上升的高度；
2. （2）依据他们测量的数据求出大树BC的高度．（参考数据：sin26.7°≈0.45，cos26.7°≈0.89，tan26.7°≈0.50）
答案解析收藏纠错 + 选题
22. (2023·济南模拟) 如图，AB为⊙O的直径，点C是⊙O上一点，CD与⊙O相切于点C，过点A作AD⊥DC，连接AC，BC.
1. （1）求证：AC是∠DAB的角平分线；
2. （2）若AD＝2，AB＝3，求AC的长.
答案解析收藏纠错 + 选题
23. (2023·济南模拟) 一文具厂接到生产一批橡皮和水笔的任务，已知该文具厂销售200个橡皮和200个水笔的利润为160元，销售100个橡皮和200个水笔的利润为130元．已知该文具厂每天生产橡皮和水笔共4500个，生产橡皮和水笔每个成本分别为2元，3元，设每天生产橡皮 $\text{[math]}$ 个，该文具厂每天生产成本为 $\text{[math]}$ 元．
1. （1）求橡皮和水笔的销售单价；
2. （2）求 $\text{[math]}$ 关于 $\text{[math]}$ 的函数关系式；
3. （3）若该文具厂每天最多投入成本为10000元，求该文具厂每天获得利润最多是多少元？
答案解析收藏纠错 + 选题
24. (2024九上·雅安期末) 如图，一次函数 $\text{[math]}$ 的图象与反比例函数 $\text{[math]}$ 的图象交于点 $\text{[math]}$ ，与y轴交于点B．
1. （1）求a，k的值；
2. （2）直线CD过点A，与反比例函数图象交于点C，与x轴交于点D，AC＝AD，连接CB．
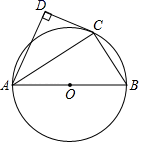
  ①求△ABC的面积；
  ②点P在反比例函数的图象上，点Q在x轴上，若以点A，B，P，Q为顶点的四边形是平行四边形，请求出所有符合条件的点P坐标．
答案解析收藏纠错 + 选题
25. (2023·济南模拟) 在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 在边 $\text{[math]}$ 上， $\text{[math]}$ ，将线段 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转至 $\text{[math]}$ ，记旋转角为 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ，以 $\text{[math]}$ 为斜边在其一侧制作等腰直角三角形 $\text{[math]}$ ．连接 $\text{[math]}$ ．
1. （1）如图1，当 $\text{[math]}$ 时，请直接写出线段 $\text{[math]}$ 与线段 $\text{[math]}$ 的数量关系；
2. （2）当 $\text{[math]}$ 时，
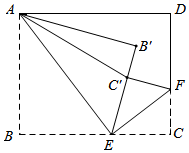
  ①如图2，（1）中线段 $\text{[math]}$ 与线段 $\text{[math]}$ 的数量关系是否仍然成立？请说明理由；
  
  ②如图3，当 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三点共线时，连接 $\text{[math]}$ ，判断四边形 $\text{[math]}$ 的形状，并说明理由．
答案解析收藏纠错 + 选题
26. (2023·济南模拟) 如图．已知抛物线 $\text{[math]}$ 经过 $\text{[math]}$ 三点，点P为直线 $\text{[math]}$ 上方抛物线上一点．
1. （1）求抛物线的解析式；
2. （2）当 $\text{[math]}$ 时，求点P的坐标；
3. （3）连接 $\text{[math]}$ ，交直线 $\text{[math]}$ 于点E，交y轴于点F；
  ①是否存在点P使 $\text{[math]}$ 与 $\text{[math]}$ 相似，若存在，求出点P的坐标，若不存在，请说明理由；
  ②若点P的坐标为 $\text{[math]}$ ，点H在抛物线上，过H作 $\text{[math]}$ 轴，交直线 $\text{[math]}$ 于点K．点Q是平面内一点，当以点E，H，K，Q为顶点的四边形是正方形时，请直接写出点Q的坐标．
答案解析收藏纠错 + 选题