山东省济宁市嘉祥县2023年中考一模数学试题

更新时间：2023-05-16 浏览次数：92 类型：中考模拟

一、单选题

1. (2023·嘉祥模拟) 实数 $\text{[math]}$ 的倒数的绝对值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 2023 D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023·嘉祥模拟) 2023年《政府工作报告》提出，“义务教育优质均衡发展”．根据预算报告，支持学前教育发展资金安排250亿元、增加20亿元，扩大普惠性教育资源供给．其中250亿元用科学记数法表示为（）

A . $\text{[math]}$ 元 B . $\text{[math]}$ 元 C . $\text{[math]}$ 元 D . $\text{[math]}$ 元

答案解析收藏纠错 + 选题
3. (2023·嘉祥模拟) 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023·东莞模拟) 使 $\text{[math]}$ 有意义的x的取值范围在数轴上表示为（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2023·德州) 如图，几何体是由六个相同的立方体构成的，则该几何体三视图中面积最大的是（）

A . 主视图 B . 左视图 C . 俯视图 D . 主视图和左视图

答案解析收藏纠错 + 选题
6. (2024·昆明模拟) 如图，已知 $\text{[math]}$ ，点E在线段AD上（不与点A，点D重合），连接CE.若∠C＝20°，∠AEC＝50°，则∠A＝（）

A . 10° B . 20° C . 30° D . 40°

答案解析收藏纠错 + 选题
7. (2023·嘉祥模拟) 小明同学对数据12，22，36.4■，52进行统计分析，发现其中一个两位数的个位数字被墨水污染已无法看清，则下列统计量与被污染数字无关的是（）

A . 平均数 B . 标准差 C . 方差 D . 中位数

答案解析收藏纠错 + 选题
8. (2023·桓台模拟) 如图，矩形ABCD中，分别以A，C为圆心，以大于 $\text{[math]}$ 的长为半径作弧，两弧相交于M，N两点，作直线MN分别交AD，BC于点E，F，连接AF，若BF＝3，AE＝5，以下结论错误的是（）

A . AF＝CF B . ∠FAC＝∠EAC C . AB＝4 D . AC＝2AB

答案解析收藏纠错 + 选题
9. (2023·嘉祥模拟) 如图， $\text{[math]}$ 是 $\text{[math]}$ 的直径，将弦 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ 得到 $\text{[math]}$ ，此时点 $\text{[math]}$ 的对应点 $\text{[math]}$ 落在 $\text{[math]}$ 上，延长 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，若 $\text{[math]}$ ，则图中阴影部分的面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023·嘉祥模拟) 如图，抛物线 $\text{[math]}$ 经过点 $\text{[math]}$ ，点 $\text{[math]}$ 从点A出发，沿抛物线运动到顶点后，再沿对称轴l向下运动，给出下列说法：
① $\text{[math]}$ ：
②抛物线的对称轴为 $\text{[math]}$ ；
③当点P，B，C构成的三角形的周长取最小值时， $\text{[math]}$ ；
④在点P从点A运动到顶点的过程中，当 $\text{[math]}$ 时， $\text{[math]}$ 的面积最大．
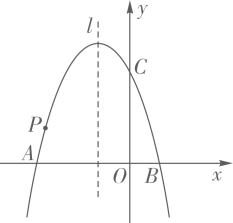
其中，所有正确的说法是（）

A . ①②③ B . ①②④ C . ②③④ D . ①③

答案解析收藏纠错 + 选题

二、填空题

11. (2024九下·赤峰模拟) 分解因式： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
12. (2023·嘉祥模拟) 在△ABC中，∠ABC=90°，BF是AC边上的中线，点D、E分别是AB、BC边上的中点，若DE=6，则BF=

答案解析收藏纠错 + 选题
13. (2024八下·西安月考) 关于x，y的方程组 $\text{[math]}$ 的解中x与y的和不小于5，则k的取值范围为．

答案解析收藏纠错 + 选题
14. (2023·嘉祥模拟) 一艘轮船位于灯塔 $\text{[math]}$ 的南偏东 $\text{[math]}$ 方向，距离灯塔30海里的 $\text{[math]}$ 处，它沿北偏东 $\text{[math]}$ 方向航行一段时间后，到达位于灯塔 $\text{[math]}$ 的北偏东 $\text{[math]}$ 方向上的 $\text{[math]}$ 处，此时与灯塔 $\text{[math]}$ 的距离约为海里．（参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

答案解析收藏纠错 + 选题
15. (2023·嘉祥模拟) 若a是不为2的有理数我们把 $\text{[math]}$ 称为a的“哈利数”．如3的“哈利数”是 $\text{[math]}$ ； $\text{[math]}$ 的“哈利数”是 $\text{[math]}$ ，已知 $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的“哈利数”， $\text{[math]}$ 是 $\text{[math]}$ 的“哈利数”， $\text{[math]}$ 是 $\text{[math]}$ 的“哈利数”，以此类推， $\text{[math]}$ ．

答案解析收藏纠错 + 选题

三、解答题

16. (2023·嘉祥模拟) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
17. (2023·宜宾模拟) 为提高学生的综合素养，某校开设了四个兴趣小组，A“健美操”、B“跳绳”、C“剪纸”、D“书法”为了了解学生对每个兴趣小组的喜爱情况，随机抽取了部分同学进行调查，并将调查结果绘制出上面不完整的统计图，请结合图中的信息解答下列问题：
1. （1）本次共调查了 ▲ 名学生；并将条形统计图补充完整；
2. （2） C组所对应的扇形圆心角为度；
3. （3）若该校共有学生1400人，则估计该校喜欢跳绳的学生人数约是；
4. （4）现选出了4名跳绳成绩最好的学生，其中有1名男生和3名女生．要从这4名学生中任意抽取2名学生去参加比赛，请用列表法或画树状图法，求刚好抽到1名男生与1名女生的概率．
答案解析收藏纠错 + 选题
18. (2023·嘉祥模拟) 如图，在▱ABCD中，点E、F分别在边AD、BC上，且∠ABE＝∠CDF．
1. （1）探究四边形BEDF的形状，并说明理由；
2. （2）连接AC，分别交BE、DF于点G、H，连接BD交AC于点O．若 $\text{[math]}$ ， AE＝4，求BC的长．
答案解析收藏纠错 + 选题
19. (2024九下·深圳开学考) 某超市采购了两批同样的冰墩墩挂件，第一批花了6600元，第二批花了8000元，第一批每个挂件的进价是第二批的1.1倍，且第二批比第一批多购进50个．
1. （1）求第二批每个挂件的进价；
2. （2）两批挂件售完后，该超市以第二批每个挂件的进价又采购一批同样的挂件，经市场调查发现，当售价为每个60元时，每周能卖出40个，若每降价1元，则每周多卖10个．求每个挂件售价定为多少元时，每周可获得最大利润，最大利润是多少?
答案解析收藏纠错 + 选题
20. (2023·嘉祥模拟) 【材料】
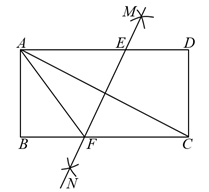
《义务教育数学课程标准2022版）》对《切线的性质与判定》的新要求是：切线长定理由“选学”改为“必学”，并新增“能用尺规作图：过圆外的一个点作圆的切线（课标课程内容中的实例76）”．根据这一要求转化为作图题为：
已知：如图， $\text{[math]}$ 及 $\text{[math]}$ 外一点P
求作：过点P的 $\text{[math]}$ 的切线
作法：
①连接 $\text{[math]}$ ，作线段 $\text{[math]}$ 的垂直平分线 $\text{[math]}$ 交 $\text{[math]}$ 于点T；
②以点T为圆心， $\text{[math]}$ 的长为半径作圆，交 $\text{[math]}$ 于点A、点B；
③作直线 $\text{[math]}$ ．
则直线 $\text{[math]}$ 就是所求作的 $\text{[math]}$ 的切线．
【问题】
1. （1）请你按照上述步骤完成作图（尺规作图，保留作图痕迹）；
2. （2）完成下面的证明．
  证明：连接 $\text{[math]}$ ．
  ∵ $\text{[math]}$ 是 $\text{[math]}$ 的直径，
  ∴ $\text{[math]}$ ▲ °．（）（填推理的依据）
  ∴ $\text{[math]}$ ．
  又∵ $\text{[math]}$ 为 $\text{[math]}$ 的半径，
  ∴直线 $\text{[math]}$ 是 $\text{[math]}$ 的切线（）（填推理的依据）．
  同理可证，直线 $\text{[math]}$ 也是 $\text{[math]}$ 的切线．
3. （3）在（2）的条件下，连接 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ 的面积等于1，求 $\text{[math]}$ 的半径．
答案解析收藏纠错 + 选题
21. (2023·嘉祥模拟) 数形结合是解决数学问题的重要方法．小爱同学学习二次函数后，对函数 $\text{[math]}$ 进行了探究．在经历列表、描点、连线步骤后，得到如图的函数图象．请根据函数图象，回答下列问题：
1. （1）观察探究：
  ①写出该函数的一条性质：；
  ②方程 $\text{[math]}$ 的解为：；
  ③若方程 $\text{[math]}$ 有四个实数根，则a的取值范围是．
2. （2）延伸思考．
  ①将函数 $\text{[math]}$ 的图象经过怎样的平移可得到函数 $\text{[math]}$ 的图象？画出平移后的图象并写出平移过程：
  ②观察平移后的图像，当 $\text{[math]}$ 时，直接写出自变量x的取值范围 ▲ ．
答案解析收藏纠错 + 选题
22. (2023·嘉祥模拟) 如图，在平面直角坐标系中，四边形 $\text{[math]}$ 为正方形，已知点 $\text{[math]}$ ，点B、C在第二象限内．
1. （1）求点B的坐标；
2. （2）将正方形 $\text{[math]}$ 以每秒1个单位的速度沿x轴向右平移t秒，若存在某一时刻、使在第一象限内点B、D两点的对应点 $\text{[math]}$ 正好落在某反比例函数的图象上，请求出此时t的值以及这个反比例函数的解析式：
3. （3）在（2）的情况下，问是否存在x轴上的点P和反比例函数图象上的点Q，使得以P、Q、 $\text{[math]}$ 四个点为顶点的四边形是以 $\text{[math]}$ 为边的平行四边形？若存在，请直接写出正确的点Q的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题