浙江省义乌市绣湖中学2022-2023学年七年级下学期数学期...

更新时间：2023-06-15 浏览次数：163 类型：期中考试

一、选择题（本题有10小题，每小题3分，共30分.）

1. (2023七下·义乌期中) 下列各式中，属于二元一次方程的是（）

A . x²+y=0 B . x= $\text{[math]}$ +1 C . $\text{[math]}$ ﹣2y=1 D . y+2x

答案解析收藏纠错 + 选题
2. (2023七下·义乌期中) 下面图形中，∠1和∠2是同位角的是（）

A . ①② B . ①③ C . ②③ D . ②④

答案解析收藏纠错 + 选题
3. (2023七下·义乌期中) 世界上最小的开花结果植物是澳大利亚的出水浮萍，它的果实像一粒微小的无花果，质量只有0.000 000 07克．数据0.000 000 07用科学记数法表示为（）

A . 0.7×10^-7 B . 7×10^-7 C . 7×10^-8 D . 7×10^-9

答案解析收藏纠错 + 选题
4. (2023七下·义乌期中) 下列运算正确的是（）

A . a⁵+a⁵＝a¹⁰ B . a⁷•a⁶＝a⁴² C . a⁴-a⁴＝a⁰ D . a⁰÷a^-1＝a

答案解析收藏纠错 + 选题
5. (2023七下·义乌期中) 下列各式能用平方差公式计算的是（）

A . （﹣a+b）（a﹣b） B . （a+b）（a﹣2b） C . （x+1）（﹣1+x） D . （﹣m﹣n）（m+n）

答案解析收藏纠错 + 选题
6. (2023七下·义乌期中) ∠A的两边与∠B的两边分别平行，∠A的度数比∠B的度数的2倍少30°，则∠A=（）

A . 30° B . 60° C . 60°或70° D . 30°或110°

答案解析收藏纠错 + 选题
7. (2023七下·义乌期中) 甲、乙两人同解方程组 $\text{[math]}$ 时，甲正确解得 $\text{[math]}$ ，乙因为抄错 $\text{[math]}$ 而解得 $\text{[math]}$ ，则代数式 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023七下·义乌期中) 若a²+2ab+b²-c²＝10，a+b+c＝5，则a+b-c的值是（　　）

A . 2 B . 5 C . 20 D . 9

答案解析收藏纠错 + 选题
9. (2023七下·义乌期中) 我们规定： $\text{[math]}$ 表示不超过 $\text{[math]}$ 的最大整数，例如： $\text{[math]}$ ， $\text{[math]}$ ，则关于 $\text{[math]}$ 和 $\text{[math]}$ 的二元一次方程组 $\text{[math]}$ 的解为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023七下·义乌期中) 如图，长为y（cm），宽为x（cm）的大长方形被分割为7小块，除阴影A，B外，其余5块是形状、大小完全相同的小长方形，其较短的边长为5cm，下列说法中正确的是（）
①小长方形的较长边为y-15；②阴影A的较短边和阴影B的较短边之和为x-y+5；③若x为定值，则阴影A和阴影B的周长和为定值；④当x＝15时，阴影A和阴影B的面积和为定值．

A . ①③④ B . ②④ C . ①③ D . ①④

答案解析收藏纠错 + 选题

二、填空题（本题有6小题，每小题3分，共18分）

11. (2023七下·义乌期中) 已知m+n＝2，mn＝-2，则（1-m）（1-n）的值为．

答案解析收藏纠错 + 选题
12. (2024七下·良庆期中) 某兴趣小组利用几何图形画出螳螂的简笔画，如图，已知∠BAC＝130°，AB∥DE，∠D＝70°，则∠ACD＝．

答案解析收藏纠错 + 选题
13. (2023七下·义乌期中) 如图，将周长为7的三角形ABC沿BC边向右平移1个单位，得到三角形DEF，则四边形ABFD的周长为 .

答案解析收藏纠错 + 选题
14. (2024七下·郑州期中) 若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
15. (2023七下·义乌期中) 计算： $\text{[math]}$ ＝．

答案解析收藏纠错 + 选题
16. (2023七下·义乌期中) F（x）表示关于x的一个五次多项式，F（a）表示x＝a时F（x）的值，若F（-2）＝F（-1）＝F（0）＝F（1）＝0，F（2）＝24，F（3）＝360，则F（4）＝．

答案解析收藏纠错 + 选题

三、解答题（本大题有8小题，第17~22小题每题6分，第23~24题每小题8分，共52分）

17. (2023七下·义乌期中)
1. （1）计算： $\text{[math]}$ ．
2. （2）化简：（2x+1）²-4x•（x-1）．
答案解析收藏纠错 + 选题
18. (2023七下·义乌期中) 解方程组：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
19. (2023七下·义乌期中) 先化简，再求值：（2x-3）²-（x+2y）（x-2y）-4y² ，其中 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
20. (2023七下·义乌期中) 如图，BC与AF相交于点E，AB∥CD，∠1＝∠2，∠3＝∠4，则AD∥BE．请说明理由.

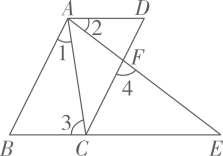
解：∵AB∥CD，

∴∠BAE＝∠4（）．

∵∠1＝∠2，

∴∠1+∠CAE＝▲ ，（等式的性质1）

即∠BAE＝∠CAD，

∴∠4＝∠CAD，（等量代换）

∵∠3＝∠4，

∴∠CAD＝∠3，（等量代换）

∴AD∥BE（）．

答案解析收藏纠错 + 选题
21. (2023七下·义乌期中) 现有三种边长分别为3，2，1的正方形卡片（如图1），分别记为Ⅰ，Ⅱ，Ⅲ．还有一个长为a，宽为b的长方形．
1. （1）如图2①，将Ⅰ放入长方形中，试用含a，b的代数式表示阴影部分的面积，并求当a＝4.5，b＝4时阴影部分的面积．
2. （2）将Ⅰ，Ⅱ两张卡片按图2②的方式，放置在长方形中，试用含a，b的代数式表示阴影部分的面积，并求当a＝4.5，b＝4时阴影部分的面积．
3. （3）将Ⅰ，Ⅱ，Ⅲ三张卡片按图2③的方式，放置在长方形中，求右上角阴影部分与左下角阴影部分周长的差．
答案解析收藏纠错 + 选题
22. (2023七下·义乌期中) 某工厂承接了一批纸箱加工任务，用如图1所示的长方形和正方形纸板（长方形的宽与正方形的边长相等）加工成如图所示的竖式与横式两种无盖的长方形纸箱．（加工时接缝材料不计）
1. （1）若该厂购进正方形纸板1000张，长方形纸板2000张．问竖式纸盒，横式纸盒各加工多少个，恰好能将购进的纸板全部用完；
2. （2）该工厂某一天使用的材料清单上显示，这天一共使用正方形纸板50张，长方形纸板a张，全部加工成上述两种纸盒，且120＜a＜136，且一个竖式纸箱成本300元，一个横式纸箱成本200元，试求在这一天加工两种纸箱时，a的所有可能值中，成本最低花费多少元？
答案解析收藏纠错 + 选题
23. (2023七下·义乌期中) 对于未知数为x，y的二元一次方程组，如果方程组的解x，y满足|x-y|＝1，我们就说方程组的解x与y具有“邻好关系”．
1. （1）方程组 $\text{[math]}$ 的解x与y（项“具有”或“不具有”）“邻好关系”；
2. （2）若方程组 $\text{[math]}$ 的解x与y具有“邻好关系”，求m的值；
3. （3）未知数为x，y的方程组 $\text{[math]}$ ，其中a与x，y都是正整数，该方程组的解x与y是否具有“邻好关系”？如果具有，请求出a的值及方程组的解；如果不具有，请说明理由．
4. （4）【拓展】若一个关于x的方程ax+b＝0（a≠0）的解为x＝b-a，则称之为“成章方程”．如：x+ $\text{[math]}$ ＝0的解为x＝- $\text{[math]}$ ，而- $\text{[math]}$ ＝ $\text{[math]}$ -1；2x+ $\text{[math]}$ ＝0的解为x＝- $\text{[math]}$ ，而- $\text{[math]}$ ＝ $\text{[math]}$ -2．
  若关于x的方程ax+b＝0（a≠0）为“成章方程”，请直接写出关于y的方程的解：a（a-b）y+2＝（b+ $\text{[math]}$ ）y．
答案解析收藏纠错 + 选题
24. (2023七下·义乌期中) 如图，直线PQ∥MN，一副三角尺（∠ABC＝∠CDE＝90°，∠ACB＝30°，∠BAC＝60°，∠DCE＝∠DEC＝45°）按如图①放置，其中点E在直线PQ上，点B，C均在直线MN上，且CE平分∠ACN．
1. （1）求∠DEQ的度数．
2. （2）如图②，若将三角形ABC绕点B以每秒3度的速度按逆时针方向旋转（A，C的对应点分别为F，G），设旋转时间为t（s）（0≤t≤60）．
  ①在旋转过程中，若边BG∥CD，求t的值．
  
  ②若在三角形ABC绕点B旋转的同时，三角形CDE绕点E以每秒2度的速度按顺时针方向旋转（C，D的对应点为H，K）．请直接写出当边BG∥HK时t的值．
答案解析收藏纠错 + 选题