吉林省松原市前郭尔罗斯蒙古族自治县2023年中考一模数学试题

更新时间：2023-05-26 浏览次数：44 类型：中考模拟

一、单选题

1. (2023·前郭尔罗斯模拟) $\text{[math]}$ 的倒数为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . 4 D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023·前郭尔罗斯模拟) 下列几何体的主视图既是轴对称图形又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2023·前郭尔罗斯模拟) 关于x的一元二次方程 $\text{[math]}$ 没有实数根，则k的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024·光明模拟) 如图，直线l₁ $\text{[math]}$ l₂ ，点C、A分别在l₁、l₂上，以点C为圆心，CA长为半径画弧，交l₁于点B，连接AB.若∠BCA＝150°，则∠1的度数为（）

A . 10° B . 15° C . 20° D . 30°

答案解析收藏纠错 + 选题
5. (2024九下·龙湾模拟) 化简 $\text{[math]}$ 的结果是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. 关于二次函数 $\text{[math]}$ 的最大值或最小值，下列说法正确的是（）

A . 有最大值4 B . 有最小值4 C . 有最大值6 D . 有最小值6

答案解析收藏纠错 + 选题

二、填空题

7. (2023·前郭尔罗斯模拟) 分解因式：a²－9b²＝；

答案解析收藏纠错 + 选题
8. (2023·前郭尔罗斯模拟) 关于x的方程 $\text{[math]}$ 的解是．

答案解析收藏纠错 + 选题
9. (2023·前郭尔罗斯模拟) 不等式 $\text{[math]}$ 的解集是．

答案解析收藏纠错 + 选题
10. (2024八下·夏邑期末) 点 $\text{[math]}$ 在一次函数 $\text{[math]}$ 的图像上，当 $\text{[math]}$ 时， $\text{[math]}$ ，则a的取值范围是．

答案解析收藏纠错 + 选题
11. (2024八下·昌邑期末) 在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 为BC边上的高， $\text{[math]}$ ，则BC的长为．

答案解析收藏纠错 + 选题
12. (2023·前郭尔罗斯模拟) 如图，约定：上方相邻两数之和等于这两个数下方剪头共同指向的数．示例：即4＋3＝7，则y＝．

答案解析收藏纠错 + 选题
13. (2024八下·任丘期末) 如图，在 △ABC中， ∠ACB=90° ， D，E，F分别为AB，BC，CA的中点．若EF的长为10，则CD的长为．

答案解析收藏纠错 + 选题
14. (2023九上·惠州月考) 在20世纪70年代，我国著名数学家华罗庚教授将黄金分割法作为一种“优选法”，在全国大规模推广，取得了很大成果.如图，利用黄金分割法，所做 $\text{[math]}$ 将矩形窗框 $\text{[math]}$ 分为上下两部分，其中E为边 $\text{[math]}$ 的黄金分割点，即 $\text{[math]}$ .已知 $\text{[math]}$ 为2米，则线段 $\text{[math]}$ 的长为米.

答案解析收藏纠错 + 选题
15. (2023·前郭尔罗斯模拟) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题

三、解答题

16. (2023·前郭尔罗斯模拟) 如图，四边形 $\text{[math]}$ 是菱形，点E，F分别在 $\text{[math]}$ 上， $\text{[math]}$ ．求证 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
17. (2024九下·新民期中) 九年级某班同学在毕业晚会中进行抽奖活动，在一个不透明的口袋中有三个完全相同的小球，把它们分别标号为1，2，3．随机摸出一个小球记下标号后放回搅匀，再从中随机摸出一个小球记下标号．规定当两次摸出的小球标号相同时中奖，求中奖的概率，请用画树状图或列表法的方法求中奖的概率．

答案解析收藏纠错 + 选题
18. (2023·前郭尔罗斯模拟) 如图，AB是⊙O的直径，PB是⊙O的切线，连接AP交⊙O于点C。点D在⊙O上，∠CDB=45°，求证：AB=BP。

答案解析收藏纠错 + 选题
19. (2023·前郭尔罗斯模拟) 如图，同学们利用所学知识去测量三江源某河段某处的宽度 $\text{[math]}$ 小宇同学在A处观测对岸点C，测得 $\text{[math]}$ ，小英同学在距点A处60米远的B点测得 $\text{[math]}$ ，请根据这些数据算出河宽 $\text{[math]}$ 精确到 $\text{[math]}$ 米， $\text{[math]}$ ， $\text{[math]}$ ．

答案解析收藏纠错 + 选题
20. (2023·前郭尔罗斯模拟) 某公司要在甲、乙两人中招聘一名职员，对两人的学历、能力、经验这三项进行了测试，各项满分均为10分，成绩高者被录用．图1是甲、乙测试成绩的条形统计图．
1. （1）分别求出甲、乙三项成绩之和，并指出会录用谁；
2. （2）若将甲、乙的三项测试成绩，按照扇形统计图（图2）各项所占之比，分别计算两人各自的综合成绩，并判断是否会改变（1）的录用结果．
答案解析收藏纠错 + 选题
21. 设函数y₁= $\text{[math]}$ ，函数y₂=k₂x+b(k₁ ， k₂ ， b是常数，k₁≠0，k₂≠0)．
1. （1）若函数y₁和函数y₂的图象交于点A(1，m)，点B(3，1)，
  ①求函数y₁ ， y₂的表达式：
  
  ②当2<x<3时，比较y₁与y₂的大小（直接写出结果）．
2. （2）若点C(2，n)在函数y₁的图象上，点C先向下平移2个单位，再向左平移4个单位，得点D，点D恰好落在函数y₁的图象上，求n的值，
答案解析收藏纠错 + 选题
22. (2023·前郭尔罗斯模拟) 如图，3×3正方形网格中，每个小正方形的顶点称为格点，点A，B都在格点上，以线段 $\text{[math]}$ 为边，按下列要求画四边形 $\text{[math]}$ ，使得点C，D都在格点上．
1. （1）图①中的四边形 $\text{[math]}$ 是轴对称图形，但不是中心对称图形
2. （2）图②中的四边形 $\text{[math]}$ 是中心对称图形，但不是轴对称图形
3. （3）图③中的四边形 $\text{[math]}$ 既是中心对称图形，也是轴对称图形
答案解析收藏纠错 + 选题
23. (2023·前郭尔罗斯模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 边上一动点， $\text{[math]}$ ，垂足为N．设A，M两点间的距离为xcm（ $\text{[math]}$ ），B，N两点间的距离为ycm（当M点和B点重合时，B，N两点间的距离为0）．
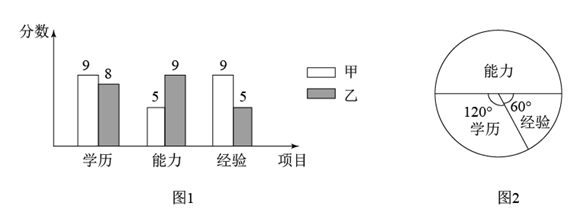
小明根据学习函数的经验，对因变量y随自变量x的变化而变化的规律进行了探究．
下面是小明的探究过程，请补充完整．
1. （1）列表：下表的已知数据是根据A，M两点间的距离x进行取点、画图、测量，分别得到的y与x的几组对应值：
  x/cm
  0
  0.5
  1
  1.5
  1.8
  2
  2.5
  3
  3.5
  4
  4.5
  5
  y/cm
  4
  3.96
  3.79
  3.47
  a
  2.99
  2.40
  1.79
  1.23
  0.74
  0.33
  0
  请你通过计算，补全表格：a=；
2. （2）描点、连线：在平面直角坐标系中，描出表中各组数值所对应的点（x，y），并画出y关于x的函数图象；
3. （3）探究性质：随着自变量x的不断增大，函数y的变化趋势：．
答案解析收藏纠错 + 选题
24. (2023·前郭尔罗斯模拟) 已知等边三角形ABC，过A点作AC的垂线l，点P为l上一动点（不与点A重合），连接CP，把线段CP绕点C逆时针方向旋转60°得到CQ，连QB．
1. （1）如图1，判断线段AP与BQ的数量关系，并说明理由；
2. （2）如图2，当点P、B在AC同侧且AP＝AC时，求证：直线PB垂直平分线段CQ；
3. （3）如图3，若等边三角形ABC的边长为4，点P、B分别位于直线AC异侧，且△APQ的面积等于 $\text{[math]}$ ，请直接写出线段AP的长度．
答案解析收藏纠错 + 选题
25. (2023·前郭尔罗斯模拟) 如图，在正方形ABCD中，AB=2，连接AC。P，Q两点分别从A，D同时出发，点P以每秒1个单位长度的速度沿线段AB向终点B运动；点Q沿折线D→A→C向终点C运动，在DA上的速度为每秒2个单位长度，在AC上的速度为每秒2 $\text{[math]}$ 个单位长度。在运动过程中，以AP，AQ为邻边作平行四边形APMQ。设运动时间为x秒，平行四边形APMQ和正方形ABCD重叠部分的图形面积为y。
1. （1）当点M在BC上时，x=
2. （2）求y关于x的函数解析式，并写出x的取值范围；
3. （3）连接MB，当0°<∠MBP<90°时，直接写出tan∠MBP= $\text{[math]}$ 时x的值。
答案解析收藏纠错 + 选题
26. (2023·前郭尔罗斯模拟) 已知抛物线 $\text{[math]}$ ．
1. （1）如图①，若抛物线图象与x轴交于点 $\text{[math]}$ ，与y轴交点 $\text{[math]}$ ．连接 $\text{[math]}$ ．
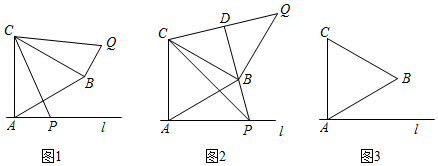
  ①求该抛物线所表示的二次函数表达式；
  ②若点P是抛物线上一动点（与点A不重合），过点P作 $\text{[math]}$ 轴于点H，与线段 $\text{[math]}$ 交于点M．是否存在点P使得点M是线段 $\text{[math]}$ 的三等分点？若存在，请求出点P的坐标；若不存在，请说明理由．
2. （2）如图②，直线 $\text{[math]}$ 与y轴交于点C，同时与抛物线 $\text{[math]}$ 交于点 $\text{[math]}$ ，以线段 $\text{[math]}$ 为边作菱形 $\text{[math]}$ ，使点F落在x轴的正半轴上，若该抛物线与线段 $\text{[math]}$ 没有交点，求b的取值范围．
答案解析收藏纠错 + 选题