|
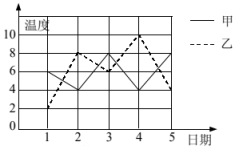
测试等级 |
A优秀 |
B良好 |
C及格 |
D不及格 |
|
人数 |
20 |
60 |
140 |
|
|
百分比 |
5% |
45% |
m |
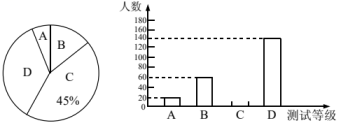
根据以上信息,回答下列问题:
|
第x天 |
5 |
10 |
15 |
20 |
|
日销售量y(件) |
50 |
60 |
70 |
80 |
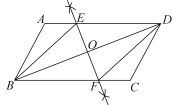
∵ , E,F分别为AC,BC的中点,
∴ ,
∵ ,
∴ ,
∴()
∴AEBF, , 又∵
,
∴ ,
∴AEBM.