一、选择题(本大题共12小题,每小题3分,共36分)
-
-
A . (5,7)
B . (7,8)
C . (8,7)
D . (7,5)
-
3.
(2023七下·泸县期中)
中国象棋具有悠久的历史,战国时期,就有了关于象棋的正式记载,如图是中国象棋棋局的一部分,如果用(2,﹣1)表示“炮”的位置,那么“将”的位置应表示为( )
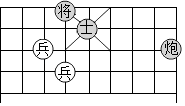
A . (﹣2,3)
B . (0,﹣5)
C . (﹣3,1)
D . (﹣4,2)
-
-
A . 有且只有一条直线垂直于已知直线
B . 从直线外一点到这条直线的垂线段,叫做这点到这条直线距离
C . 互相垂直的两条线段一定相交
D . 直线c外一点A与直线c上各点连接而成的所有线段中最短线段的长是3cm,则点A到直线c的距离是3cm
-
6.
(2023七下·泸县期中)
如图所示,下列能判定AB∥CD的条件有( )

①∠1=∠2;②∠3=∠4;③∠B=∠5;④∠B+∠BCD=180°;⑤∠5=∠D
A . 1个
B . 2个
C . 3个
D . 4个
-
A . -6是-36的算术平方根
B . 5是(-5)2的算术平方根
C . 64的立方根是±4
D .  一定是正数
一定是正数
-
A . 3个
B . 4个
C . 5个
D . 6个
-
A . -2
B . 2
C . 4
D . -4
-
A . ﹣1
B . 1
C . ﹣2
D . 4
-
11.
(2023七下·泸县期中)
中国古代数学著作《算法统宗》中记载了这样一个题目:九百九十九文钱,甜果苦果买一千,四文钱买苦果七,十一文钱九个甜,甜苦两果各几个?其大意是:用九百九十九文钱共买了一千个苦果和甜果,其中四文钱可以买苦果七个,十一文钱可以买甜果九个.问:苦、甜果各有几个?设苦果有

个,甜果有

个,则可列方程组为( )
-
12.
(2023七下·泸县期中)
在平面直角坐标系xOy中,对于点P(x,y)我们把P(-y+1,x+1)叫做点P的伴随点,已知A
1的伴随点为A
2 , 点A
2的伴随点为A
3 , 点A
3的伴随点为A
4 , 这样依次得到A
1 , A
2 , A
3 , …A
n , 若点A
1的坐标为(3,1),则点A
2023的坐标为 ( )
A . (0,4)
B . (3,1)
C . (-3,1)
D . (0,-2)
二、填空题(本大题共4小题,每题3分,共计12分)
-
13.

的平方根是
.
-
-
-
16.
(2023七下·泸县期中)
对于实数a、b,定义min{a,b}的含义为:当a<b时,min{a,b}=a;当a>b时,min{a,b}=b,例如:min{1,-2}=-2.已知min{

, a}=a,min{

, b}=

, 且a和b为两个连续正整数,则a-b的值为
.
三、解答题(本大题共3个小题,17题9分,18、19每题4分,20题5分,共22分)
-
-
(1)

.
-
(2)
(-1)
2017×(-3)-|

-3|+

.
-
-
-
四、 解答题(21题6分,22、23题每8分,24题6分、共28分)
-
-
-
(2)
求

的平方根
-
-
23.
(2023七下·泸县期中)
完成推理填空:如图在△ABC中,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠C.

解:∵∠1+∠2=180°( ),
▲ +∠EFD=180°(邻补角定义),
∴▲ (同角的补角相等)
∴AB∥▲ (内错角相等,两直线平行)
∴∠ADE=∠3( )
∵∠3=∠B(已知)
∴ ▲ (等量代换)
∴▲ ∥BC(同位角相等,两直线平行)
∴∠AED=∠C( )
-
24.
(2023七下·泸县期中)
如图,点B、E分别在AC、DF上,BD、CE均与AF相交,∠1=∠2, ∠C=∠D.
求证:AC//DF.

五、解答题(25题10分,26题12分,共22分)
-
25.
(2023七下·泸县期中)
目前节能灯在城市已基本普及,今年四川省面向县级及农村地区推广,为相应号召,某商场计划用3800元购进节能灯120只,这两种节能灯的进价、售价如下表:
| 类别/单价 | 成本价 | 销售价(元/箱) |
| 甲 | 25 | 30 |
| 乙 | 45 | 60 |
-
-
(2)
全部售完120只节能灯后,该商场获利润多少元?
-
-
(1)
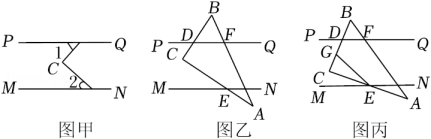
若∠1与∠2都是锐角,如图甲,写出∠C与∠1,∠2之间的数量关系并说明原因;
-
(2)
若把一块三角尺(∠A=30°,∠C=90°)按如图乙方式放置,点D,E,F是三角尺的边与平行线的交点,若∠AEN=∠A,求∠BDF的度数;
-
(3)
将图乙中的三角尺进行适当转动,如图丙,直角顶点C始终在两条平行线之间,点G在线段CD上,连接EG,且有∠CEG=∠CEM,求∠GEN与∠BDF之间的数量关系.
 C .
C .  D .
D .