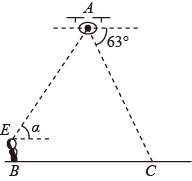
 B .
B .  C .
C .  D .
D . 
 D .
D . 
![]()
|
步数/步 |
频数 |
频率 |
|
|
8 |
|
|
|
15 |
|
|
|
12 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
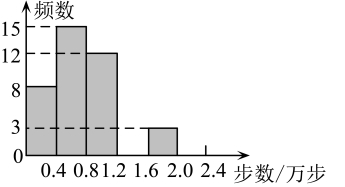
请根据以上信息,解答下列问题:


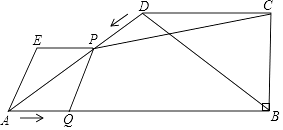
根据题意解答下列问题:
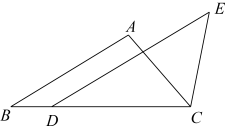
一次数学综合实践活动课上,小慧发现并证明了关于三角形角平分线的一个结论.如图1,已知AD是△ABC的角平分线,可证=
.小慧的证明思路是:如图2,过点C作CE∥AB,交AD的延长线于点E,构造相似三角形来证明
=
.

①若AC=1,AB=2,求DE的长;
②若BC=m,∠AED= , 求DE的长(用含m,
的式子表示).