
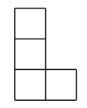
 B .
B .  C .
C . 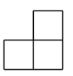 D .
D . 

|
x |
… |
-1 |
0 |
1 |
2 |
… |
|
|
y=ax2+bx+c |
… |
m |
-1 |
-1 |
n |
t |
… |
且当x=-时,与其对应的函数值y>0,有下列结论:①abc>0;②当x>1时,y随x的增大而减小;③关于x的方程ax2+bx+c=t的两个根是
和1-
;④m+n>
. 其中正确的结论是.(填写序号)
![]()
(I)解不等式①,得 ▲ ;
(Ⅱ)解不等式②,得 ▲ ;
(Ⅲ)将不等式①和②的解集在数轴上表示出来:
![]()
(Ⅳ)原不等式组的解集为 ▲ .

|
组别 |
分数段 |
人数 |
|
A |
x<60 |
2 |
|
B |
60≤x<75 |
5 |
|
C |
75≤x<90 |
a |
|
D |
x≥90 |
12 |
请根据上述信息解答下列问题:


如图2,平行四边形ABCD,AB=5,BC=4,点E边AB上,点F在边BC的延长线上,连接AF与DE交于点O,当∠FOD=∠B时,求的值;
如图3,菱形ABCD中,(m>2),点E在边AB上,点F是BC延长线上一点,且满足
, 连接AF与DE交于点O时,∠DAO=∠AED;直接写出cos∠ABF的值.(用含m的式子表示)

