北京市海淀区一零一集团2022-2023学年七年级下学期数学...

更新时间：2023-09-21 浏览次数：99 类型：期中考试

一、单选题

1. (2024七下·梁园期末) 4的算术平方根是（）

A . -2 B . 2 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023七下·海淀期中) 在平面直角坐标系 $\text{[math]}$ 中，点 $\text{[math]}$ 在（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
3. (2024七下·北京市期中) 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023八上·海淀开学考) 已知二元一次方程x+7y=5，用含x的代数式表示y，正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023七下·海淀期中) 如图，直线 $\text{[math]}$ ， $\text{[math]}$ 相交于点 $\text{[math]}$ ，分别作 $\text{[math]}$ ， $\text{[math]}$ 的平分线 $\text{[math]}$ ， $\text{[math]}$ ． $\text{[math]}$ ，则 $\text{[math]}$ 的度数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023七下·海淀期中) 图，面积为7的正方形ABCD的顶点A在数轴上，且表示的数为1，若点E在数轴上（点E在点A的右侧），且AB＝AE，则点E所表示的数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 1+ $\text{[math]}$ D . $\text{[math]}$ +2

答案解析收藏纠错 + 选题
7. (2023七下·海淀期中) 如图，四边形 $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 延长线上一点，下列推理正确的是（）

A . 如果 $\text{[math]}$ 那么 $\text{[math]}$ B . 如果 $\text{[math]}$ ，那么 $\text{[math]}$ C . 如果 $\text{[math]}$ ，那么 $\text{[math]}$ D . 如果 $\text{[math]}$ ，那么 $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023七下·海淀期中) 关于式子 $\text{[math]}$ （ $\text{[math]}$ 为实数），下列结论中错误的是（）

A . 式子 $\text{[math]}$ 一定有平方根 B . 当 $\text{[math]}$ 时，式子 $\text{[math]}$ 有最小值 C . 无论 $\text{[math]}$ 为何值，式子 $\text{[math]}$ 的值一定是有理数 D . 式子 $\text{[math]}$ 的算术平方根一定大于等于1

答案解析收藏纠错 + 选题
9. (2023七下·海淀期中) 已知方程组 $\text{[math]}$ ，则x-y的值是（）

A . 2 B . -2 C . 0 D . -1

答案解析收藏纠错 + 选题
10. (2023七下·海淀期中) 在平面直角坐标系 $\text{[math]}$ 中，对于点 $\text{[math]}$ ，如果点 $\text{[math]}$ 的纵坐标满足 $\text{[math]}$ ，那么称点 $\text{[math]}$ 为点 $\text{[math]}$ 的“关联点”．如果点 $\text{[math]}$ 的关联点 $\text{[math]}$ 坐标为 $\text{[math]}$ ，则点 $\text{[math]}$ 的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ 或 $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2023七下·海淀期中) 在平面直角坐标系中，将点 $\text{[math]}$ 向上平移5个单位长度得到点B，则点B坐标为

答案解析收藏纠错 + 选题
12. (2023七下·海淀期中) 举例说明命题“两个无理数 $\text{[math]}$ 、 $\text{[math]}$ 的和一定是无理数”是假命题， $\text{[math]}$ ， $\text{[math]}$ ．

答案解析收藏纠错 + 选题
13. (2024七下·北京市期中) 已知点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，直线 $\text{[math]}$ 轴，并且 $\text{[math]}$ ，则点 $\text{[math]}$ 的坐标为．

答案解析收藏纠错 + 选题
14. (2023七下·海淀期中) 某学生上学路线如图所示，他总共拐了三次弯，最后行车路线与开始的路线相互平行，已知第一次转过的角度，第三次转过的角度，则第二次拐弯角（∠1）的度数是．

答案解析收藏纠错 + 选题
15. (2023七下·海淀期中) 我国古代数学著作《增删算法统宗》记载“绳索量竿”问题：“一条竿子一条索，索比竿子长一托．折回索子却量竿，却比竿子短一托．”其大意为，现有一根竿和一条绳索，用绳索去量竿，绳索比竿长6尺；如果将绳索对半折后再去量竿，就比竿短6尺．设绳索长x尺，竿长y尺，可列出符合题意的方程组为．

答案解析收藏纠错 + 选题

16. (2023七下·海淀期中) 在我校初一年级举行的“古诗词大赛”中，有小晴、小贝、小敏三位同学进入最后冠军的角逐．决赛共分为六轮，规定：每轮分别决出第1，2，3名（不并列），对应名次的得分分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ （ $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 均为正整数）；选手最后得分为各轮得分之和，得分最高者为冠军．下表是三位选手在每轮比赛中的部分得分情况：

	第一轮	第二轮	第三轮	第四轮	第五轮	第六轮	最后得分
小晴	$\text{[math]}$						26
小贝					$\text{[math]}$	$\text{[math]}$	12
小敏		$\text{[math]}$					10

根据题中所给信息，下列说法正确的是．（填序号）

①可求得 $\text{[math]}$ ；

②每轮比赛第二名得分为2分；

③小敏一定有两轮（且只有两轮）获得第3名；

④小贝每轮比赛都没有获得第1名．

答案解析收藏纠错 + 选题

三、解答题

17. (2023九上·兴宁开学考) 计算： $\text{[math]}$

答案解析收藏纠错 + 选题
18. (2023七下·海淀期中) 求出下列等式中 $\text{[math]}$ 的值．
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
19. (2023七下·闽清期末) 解方程组： $\text{[math]}$

答案解析收藏纠错 + 选题
20. (2023七下·海淀期中) 完成下面的解题过程．
已知：如图， $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ，求 $\text{[math]}$ ．

解：∵ $\text{[math]}$ （                ）
又∵ $\text{[math]}$
∴ $\text{[math]}$
∴ $\text{[math]}$ （                ）
∴ $\text{[math]}$        ▲   $\text{[math]}$ （                ）
∵ $\text{[math]}$
∴ $\text{[math]}$
∵ $\text{[math]}$ 平分 $\text{[math]}$
∴ $\text{[math]}$
∴ $\text{[math]}$        ▲   $\text{[math]}$ ．

答案解析收藏纠错 + 选题
21. (2023七下·海淀期中) 如图所示的是天安门周围的景点分布示意图，若以正东、正北方向为 $\text{[math]}$ 轴、 $\text{[math]}$ 轴的正方向建立坐标系，表示电报大楼的点的坐标为 $\text{[math]}$ ，表示王府井的点的坐标为 $\text{[math]}$ ，请解决下面的问题：
1. （1）在图中画出相应的平面直角坐标系，并写出美术馆的坐标；
2. （2） “天安门—故宫—景山”所在的直线称为北京城的中轴线，在王府井的小奇同学如果要在最短的时间内（速度相同）赶到中轴线上，则小奇应该直接到达中轴线上的点的坐标为，理论依据为．
答案解析收藏纠错 + 选题
22. (2023七下·海淀期中) 我们规定用 $\text{[math]}$ 表示一对数对，给出如下定义：记 $\text{[math]}$ ， $\text{[math]}$ （其中 $\text{[math]}$ ， $\text{[math]}$ ），将 $\text{[math]}$ 与 $\text{[math]}$ 称为数对 $\text{[math]}$ 的一对“和谐数对”．例如： $\text{[math]}$ 的一对“和谐数对”为 $\text{[math]}$ 和 $\text{[math]}$ ．
1. （1）数对 $\text{[math]}$ 的一对“和谐数对”是；
2. （2）若数对 $\text{[math]}$ 的一对“和谐数对”相同，则 $\text{[math]}$ 的值为；
3. （3）若数对 $\text{[math]}$ 的一个“和谐数对”是 $\text{[math]}$ ，直接写出 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
23. (2023七下·海淀期中) 小明和小智在游戏中把五个相同的曲别针环环相扣，每个曲别针的长度为15毫米，厚度为1毫米，如果把这个曲别针环拉直（如图所示），则这个曲别针环拉直后长为多少呢？两位同学思考后分别给出了思路：


小明：如下图，我只要分别把后面的每段长度算出来，相加就可以；



小智：我采用的是平移的思想，先假设五个曲别针不是环环相扣，而是紧密排列成下图



此时总长为 $\text{[math]}$ 毫米，每两个曲别针环环相扣，相当于把右边的曲别针向左平移了一定的长度，然后用 $\text{[math]}$ 减去所有的平移长度就可以算出来了．

请完成下面的问题：
1. （1）这个曲别针环长为毫米；
2. （2）请根据小智的思路列出相应的算式：．
答案解析收藏纠错 + 选题
24. (2023七下·海淀期中) 某校组织“衫衫来了，爱心义卖”活动，购进了黑白两种纯色的文化衫共200件，进行DIY手绘设计后出售，所获利润全部捐给“太阳村”．每种文化衫的成本和售价如下表：

白色文化衫
黑色文化衫
成本（元）
     6
    8
售价（元）
      20
    25
假设文化衫全部售出，共获利3040元，求购进两种文化衫各多少件？

答案解析收藏纠错 + 选题
25. (2023七下·海淀期中)
1. （1）下面是小李探索 $\text{[math]}$ 的近似值的过程，请补充完整：
  我们知道面积是2的正方形的边长是 $\text{[math]}$ ，且 $\text{[math]}$ ．设 $\text{[math]}$ ，可画出如下示意图．
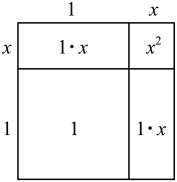
  由面积公式，可得 $\text{[math]}$ ．
  略去 $\text{[math]}$ ，得方程 $\text{[math]}$ ．
  解得 $\text{[math]}$ ．即 $\text{[math]}$ ．
2. （2）容易知道 $\text{[math]}$ ，设 $\text{[math]}$ ，类比（1）的方法，探究 $\text{[math]}$ 的近似值．（画出示意图，标明数据，并写出求解过程）
答案解析收藏纠错 + 选题
26. (2023七下·海淀期中) 平面内有两个锐角 $\text{[math]}$ 与 $\text{[math]}$ ，点 $\text{[math]}$ 在直线 $\text{[math]}$ 的上方， $\text{[math]}$ 保持不动，且 $\text{[math]}$ 的一边 $\text{[math]}$ ，另一边 $\text{[math]}$ 与直线 $\text{[math]}$ 相交于点 $\text{[math]}$ ．
1. （1）若 $\text{[math]}$ ， $\text{[math]}$ ，且位置如图1，当点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 在同一条直线上（即点 $\text{[math]}$ 与点 $\text{[math]}$ 重合）时， $\text{[math]}$ $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，当点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 不在同一条直线上，画出图形并求 $\text{[math]}$ 的度数（用含 $\text{[math]}$ ， $\text{[math]}$ 的式子表示）．
答案解析收藏纠错 + 选题
27. (2023七下·海淀期中) 对于实数 $\text{[math]}$ ， $\text{[math]}$ 表示不小于 $\text{[math]}$ 的最小整数，例如： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．点 $\text{[math]}$ 是 $\text{[math]}$ 轴右侧的点，已知点 $\text{[math]}$ ， $\text{[math]}$ ，我们把 $\text{[math]}$ （三角形 $\text{[math]}$ ）叫做点 $\text{[math]}$ 的取整三角形．
1. （1）已知点 $\text{[math]}$ ，直接写出点 $\text{[math]}$ 的坐标；
2. （2）已知点 $\text{[math]}$ ，且点 $\text{[math]}$ 的取整三角形面积为5，直接写出 $\text{[math]}$ 的取值范围：；
3. （3）若点 $\text{[math]}$ 的取整三角形面积为2，请在下面的坐标系中画出所有满足条件的点 $\text{[math]}$ 的区域（用阴影表示，能取到的边界用实线表示，不能取到的边界用虚线表示）．
答案解析收藏纠错 + 选题