福建省福州晋安区2022-2023学年七年级下册数学期末考试...

更新时间：2023-07-28 浏览次数：74 类型：期末考试

一、选择题：本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1. (2023七下·晋安期末) 一元一次方程 $\text{[math]}$ 的解是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023七下·晋安期末) 若 $\text{[math]}$ ，是方程 $\text{[math]}$ 的一个解，则k的值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 1 D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023七下·晋安期末) 只使用下列正多边形中的一种铺满地面，这种正多边形可以是（）

A . 正五边形 B . 正六边形 C . 正七边形 D . 正八边形

答案解析收藏纠错 + 选题
4. (2023七下·晋安期末) 每年12月2日是“全国交通安全日”.下列交通标志图案（不含文字说明）既是轴对称图形又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2023七下·晋安期末) 已知小明的家A、小青的家B、小红的家C构成一个三角形 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，则小青的家B与小红的家C之间的距离不可能是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023七下·晋安期末) 如图，将三角形纸片 $\text{[math]}$ 剪掉一角得 $\text{[math]}$ 与四边形 $\text{[math]}$ ，设 $\text{[math]}$ 的外角和、四边形 $\text{[math]}$ 的外角和分别为 $\text{[math]}$ 、 $\text{[math]}$ ，则下列正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023七下·晋安期末) 如图，将一块直角三角尺 $\text{[math]}$ 绕直角顶点O按顺时针方向旋转 $\text{[math]}$ 度后得到 $\text{[math]}$ ，若 $\text{[math]}$ ，则旋转角 $\text{[math]}$ 等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023七下·晋安期末) 若3a+2b=0，且a＜0，则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2023七下·晋安期末) 如图，点A、B分别在锐角 $\text{[math]}$ 的边 $\text{[math]}$ 、 $\text{[math]}$ 上，射线 $\text{[math]}$ 在 $\text{[math]}$ 的内部，点D、E在射线 $\text{[math]}$ 上，若 $\text{[math]}$ ，则 $\text{[math]}$ 等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023七下·晋安期末) 已知 $\text{[math]}$ 中每一个数值只能取2、0、 $\text{[math]}$ 中的一个，且满足 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 中0的个数是（）

A . 20 B . 19 C . 18 D . 17

答案解析收藏纠错 + 选题

二、填空题：本大题共6小题，每小题4分，共24分.

11. (2023七下·晋安期末) “a与3的差是非负数”用不等式表示为.

答案解析收藏纠错 + 选题
12. (2023七下·晋安期末) 若 $\text{[math]}$ ，则 $\text{[math]}$ （试用含x的代数式表示y）.

答案解析收藏纠错 + 选题
13. (2023七下·晋安期末) 正十边形的每个内角是度.

答案解析收藏纠错 + 选题
14. (2023七下·晋安期末) 我国古代数学家梅縠成的《增删算法统宗》中有题如下：一千官军一千布，一官四疋无零数.四军才分布一疋，请问官军多少数.其大意为：今有1000官兵分1000疋布，1官分4疋，4兵分1疋，请问官兵各几人?若设官x人，兵y人，依题意可列方程组为.

答案解析收藏纠错 + 选题
15. (2023七下·晋安期末) 如图，将四边形纸片 $\text{[math]}$ 沿 $\text{[math]}$ 折叠，点A、D分别落在点 $\text{[math]}$ 、 $\text{[math]}$ 处.若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 与 $\text{[math]}$ 之间的数量关系可用等式表示为.

答案解析收藏纠错 + 选题
16. (2023七下·晋安期末) 若关于x、y的方程组 $\text{[math]}$ 的解是 $\text{[math]}$ ，则关于m、n的方程组 $\text{[math]}$ 的解是.

答案解析收藏纠错 + 选题

三、解答题：本大题共9小题，共86分.解答应写出文字说明，证明过程或演算步骤.

17. (2023七下·晋安期末) 解方程： $\text{[math]}$ .

答案解析收藏纠错 + 选题
18. (2023七下·晋安期末) 解方程组： $\text{[math]}$

答案解析收藏纠错 + 选题
19. (2023七下·晋安期末) 解不等式组 $\text{[math]}$ ，并把解集在数轴上表示出来.

答案解析收藏纠错 + 选题
20. (2023七下·晋安期末) 如图，在网格图中， $\text{[math]}$ 在 $\text{[math]}$ 外， $\text{[math]}$ .
1. （1）在网格图中，画出 $\text{[math]}$ 关于 $\text{[math]}$ 的轴对称图形 $\text{[math]}$ ；再画出 $\text{[math]}$ 关于 $\text{[math]}$ 的轴对称图形 $\text{[math]}$ ；
2. （2）在（1）的条件下，若 $\text{[math]}$ 可以看作是由 $\text{[math]}$ 一次性运动变换得来的，试说明该如何进行运动变换?
答案解析收藏纠错 + 选题
21. (2023七下·晋安期末) 在等式 $\text{[math]}$ 中，当 $\text{[math]}$ 时， $\text{[math]}$ .
1. （1）求b的值；
2. （2）若关于x的一元一次不等式组 $\text{[math]}$ 恰有3个整数解，求a的最小值.
答案解析收藏纠错 + 选题
22. (2023七下·晋安期末) 若x为实数，则 $\text{[math]}$ 表示不大于x的最大整数，例如 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 等. $\text{[math]}$ 是大于x的最小整数，对任意的实数x都满足不等式 $\text{[math]}$ ①.利用这个不等式①，求满足 $\text{[math]}$ 的所有解.

答案解析收藏纠错 + 选题
23. (2023七下·晋安期末) 如图，在直角三角形 $\text{[math]}$ 中， $\text{[math]}$ ，线段 $\text{[math]}$ 是由线段 $\text{[math]}$ 绕点A按逆时针旋转90°得到的， $\text{[math]}$ 是由 $\text{[math]}$ 沿 $\text{[math]}$ 方向平移得到，且直线 $\text{[math]}$ 过点D.
1. （1）求 $\text{[math]}$ 的大小；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 扫过的面积.
答案解析收藏纠错 + 选题
24. (2023七下·晋安期末) 某校为推进五育并举，增强学生身体素质，拟开设篮球、足球校本选修课程，现需要购进一批篮球和足球.已知购买2个篮球和1个足球共需费用330元；购买5个篮球和2个足球共需费用780元.
1. （1）求篮球和足球的单价各是多少元?
2. （2）在开设选修课程前，学校拟用810元购买若干个篮球和足球进行教学评估，且两种球均要购买，有哪几种购买方案?
3. （3）若正式开设选修课程需要采购篮球、足球共60个，并要求篮球不少于19个，且总费用不超过6050元，试根据不同的购买方案，确定如何购买，才能使总费用最少，并求出费用的最小值.
答案解析收藏纠错 + 选题
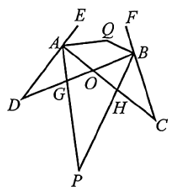
25. (2023七下·晋安期末) 阅读材料：两个三角形各有一个角互为对顶角，这两个三角形叫做对顶三角形.
解决问题：如图， $\text{[math]}$ 与 $\text{[math]}$ 是对顶三角形.
1. （1）试说明： $\text{[math]}$ ；
2. （2）试利用上述结论解决下列问题：
  若 $\text{[math]}$ 、 $\text{[math]}$ 分别平分 $\text{[math]}$ 与 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，
  
  ①求 $\text{[math]}$ 的度数（用含m、n的代数式表示）；
  
  ②若 $\text{[math]}$ 、 $\text{[math]}$ 分别平分 $\text{[math]}$ 与 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的取值范围.
答案解析收藏纠错 + 选题