黑龙江省双鸭山市2022-2023学年八年级下册数学期末试卷

更新时间：2024-07-14 浏览次数：40 类型：期末考试

一、选择题（每题3分，满分30分）

1. (2023八下·双鸭山期末) 下列各式计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023八下·双鸭山期末) 满足下列条件的 $\text{[math]}$ ，其中不是直角三角形的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

3. (2023八下·双鸭山期末) 某校男子足球队的年龄分布如下表：

年龄/岁	13	14	15	16	17	18
人数	2	6	8	3	2	1

则这些队员年龄的平均数是（）

A . 13 B . 14 C . 14.5 D . 15

答案解析收藏纠错 + 选题

4. (2023八下·双鸭山期末) 同一平面直角坐标系中，一次函数 $\text{[math]}$ 与 $\text{[math]}$ （m，n为常数）的图象可能是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2023八下·双鸭山期末) 如图，在正方形ABCD中，E是对角线上一点，连接AE，CE，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . 105° B . 120° C . 135° D . 150°

答案解析收藏纠错 + 选题
6. (2024八下·铁锋期中) 我们规定：对于任意的正数m，n的运算“ $\text{[math]}$ ”为当 $\text{[math]}$ 时， $\text{[math]}$ ；当 $\text{[math]}$ 时， $\text{[math]}$ ，其他运算符号意义不变，按上述规定，计算 $\text{[math]}$ 的结果为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023八下·双鸭山期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，按以下步骤作图：①以点B为圆心，任意长为半径作弧，分别交BA，BC于M，N两点；②分别以点M，N为圆心，以大于 $\text{[math]}$ 的长为半径作弧，两弧相交于点P；③作射线BP，交边AC于点D.若 $\text{[math]}$ ， $\text{[math]}$ ，则线段CD的长为（）

A . 3 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023八下·双鸭山期末) 数形结合是解决数学问题常用的思想方法.如图，直线y=x+5和直线y=ax+b，相交于点P ，根据图象可知，方程x+5=ax+b的解是（）

A . x=20 B . x=5 C . x=25 D . x=15

答案解析收藏纠错 + 选题
9. (2023八下·双鸭山期末) 如图，在△ABC中，D、E分别为AB、AC的中点，CF平分∠ACB，交DE于点F，若AC＝4，则EF的长为（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
10. (2023八下·双鸭山期末) 某市举办中小学生春季越野大赛，小明、小颖两名同学同时从起点出发，他们所跑的路程y（单位：千米）与时间x（单位：分钟）的函数关系如图所示.小刚由图象得出下列信息：①出发后，途中小明和小颖有3次相遇；②小明在比赛中的速度始终比小颖快，所以小明先到达终点；③比赛开始20分钟时小颖跑了2500米；④越野全程为6000米.在小刚得出的信息中，正确的有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题（每题3分，满分24分）

11. (2023八下·双鸭山期末) 在函数 $\text{[math]}$ 中，自变量x的取值范围为.

答案解析收藏纠错 + 选题
12. (2024八下·银川期中) 已知 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
13. (2023八下·双鸭山期末) 从甲、乙、丙三人中选一人参加环保知识决赛，经过两轮测试，他们的平均成绩都是88.9，方差分别是 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，你认为最适合参加决赛的选手是（填“甲”“乙”或“丙”）.

答案解析收藏纠错 + 选题
14. (2023八下·双鸭山期末) 如图所示，直线a经过正方形ABCD的顶点A，分别过正方形的顶点B、D作BF⊥a于点F，DE⊥a于点E，若DE＝5，BF＝8则EF的长为.

答案解析收藏纠错 + 选题
15. (2023八下·双鸭山期末) 如图，已知直线 $\text{[math]}$ 与x轴、y轴分别交于点A和点B，M是OB上一点，若将 $\text{[math]}$ 沿AM翻折，点B恰好落在x轴上的点 $\text{[math]}$ 处，则直线AM所对应的函数解析式是.

答案解析收藏纠错 + 选题
16. (2023八下·双鸭山期末) 小明在某次投篮中刚好把球打到篮板的点D处后进球.已知小明与篮板底的距离 $\text{[math]}$ 米，眼睛与地面的距离 $\text{[math]}$ 米，眼睛与篮板的点D的距离 $\text{[math]}$ 米，则点D到地面的距离CD是米.

答案解析收藏纠错 + 选题
17. (2023八下·茶陵期末) 如图，在菱形 $\text{[math]}$ 中，对角线 $\text{[math]}$ 交于点 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 于点 $\text{[math]}$ ，已知BO=4，S_菱形ABCD=24，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2023八下·双鸭山期末) 如图，点 $\text{[math]}$ 位于坐标原点，点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， …， $\text{[math]}$ 在y轴的正半轴上，点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， …， $\text{[math]}$ 在第一象限，点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， …， $\text{[math]}$ 在第二象限，四边形 $\text{[math]}$ 、四边形 $\text{[math]}$ 、四边形 $\text{[math]}$ ……四边形 $\text{[math]}$ 都是菱形， $\text{[math]}$ .若 $\text{[math]}$ ，且 $\text{[math]}$ ，则点 $\text{[math]}$ 的横坐标为.

答案解析收藏纠错 + 选题

三、解答题（满分66分）

19. (2024八下·巴彦期末) 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ ， $\text{[math]}$ .

答案解析收藏纠错 + 选题
20. (2023八下·双鸭山期末) 如图，在▱ABCD中，已知 $\text{[math]}$ .
1. （1）作 $\text{[math]}$ 的平分线交BC于点E，在AD上截取 $\text{[math]}$ ，连接EF；（要求：尺规作图，保留作图痕迹，不写作法.）
2. （2）直接写出四边形ABEF的形状.
答案解析收藏纠错 + 选题
21. (2023八下·双鸭山期末) 某校八年级甲、乙两班各有学生50人，为了解这两个班学生的身体素质情况，进行了抽样调查，过程如下，请补充完整.
⑴收集数据
从甲、乙两个班各随机抽取10名学生进行身体素质测试，测试成绩（百分制）如下：
甲班：65 75 75 80 60 50 75 90 85 65
乙班：90 55 80 70 55 70 95 80 65 70
⑵整理、描述数据
按如下分数段整理、描述这两组样本数据：

成绩x/分
          $\text{[math]}$
          $\text{[math]}$
          $\text{[math]}$
          $\text{[math]}$
          $\text{[math]}$
甲班
1
3
3
2
1
乙班
2
1
m
2
n
则 $\text{[math]}$       ▲       ， $\text{[math]}$       ▲      ；
⑶分析数据
①两组样本数据的平均数、中位数、众数如下表：

班级
平均数
中位数
众数
甲班
72
x
75
乙班
73
70
y
则 $\text{[math]}$       ▲       ， $\text{[math]}$       ▲      .
②若规定测试成绩在80分（含80分）以上的学生的身体素质为优秀，请估计乙班50名学生中身体素质为优秀的学生人数.

答案解析收藏纠错 + 选题
22. (2023八下·双鸭山期末) 如图，正方形纸片ABCD的边长为3，点E、F分别在边BC、CD上，将AB、AD分别沿AE、AF折叠，点B、D恰好都落在点G处，已知BE=1，求EF的长.

答案解析收藏纠错 + 选题
23. (2023八下·双鸭山期末) 联想中垂线的性质，我们可引入如下概念：
定义：到三角形的两个顶点距离相等的点，叫做此三角形的“智慧心”.
1. （1）举例：如图①，在 $\text{[math]}$ 中， $\text{[math]}$ ，判断：点 $\text{[math]}$ （填“是”或“不是”） $\text{[math]}$ 的“智慧心”；
2. （2）应用：如图②，若CD为等边三角形ABC的高，“智慧心”P在高CD上，且 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为；
3. （3）探究：已知 $\text{[math]}$ 为直角三角形， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， “智慧心”P在AC边上，则PA的长为.
答案解析收藏纠错 + 选题
24. (2023八下·双鸭山期末) 某药店销售A，B两种型号的口罩，已知销售80只A型和45只B型的利润为21元；销售40只A型和60只B型的利润为18元.
1. （1）求每只A型口罩和每只B型口罩的销售利润；
2. （2）该药店计划一次购进两种型号的口罩共2000只，其中B型口罩的进货量不少于A型口罩的进货量且不超过它的3倍，设购进A型口罩x只，这2000只口罩的销售总利润为y元，求y关于x的函数关系式，并求出自变量x的取值范围；
3. （3）在（2）的条件下，该药店购进A型、B型口罩各多少只，才能使销售总利润最大？
答案解析收藏纠错 + 选题
25. (2023八下·双鸭山期末)
1. （1）【感知】
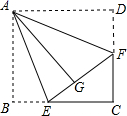
  如图①，四边形ABCD和四边形CEFG均为正方形.BE与DG的数量关系为；
2. （2）【拓展】
  如图②，四边形ABCD和四边形CEFG均为菱形，且 $\text{[math]}$ .请判断BE与DG的数量关系，并说明理由；
3. （3）【应用】
  如图③，四边形ABCD和四边形CEFG均为菱形，点E在边AD上，点G在AD的延长线上.若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的面积为9，求菱形CEFG的面积.
答案解析收藏纠错 + 选题
26. (2023八下·双鸭山期末) 如图所示，在平面直角坐标系中，四边形ABCD是菱形，点A的坐标为 $\text{[math]}$ ，点B，C在x轴上，点D在y轴上.
1. （1）求点B的坐标；
2. （2）动点P以每秒1个单位长度的速度从点O出发，沿射线OB方向运动，设点P运动的时间为t秒，连接PD，BD，设 $\text{[math]}$ 的面积为 $\text{[math]}$ ，求S与t的函数关系式（请直接写出自变量t的取值范围）；
3. （3）在（2）的条件下，平面内是否存在点Q，使以A，C，P，Q为顶点的四边形为矩形？若存在，请直接写出点Q的坐标；若不存在，请说明理由.
答案解析收藏纠错 + 选题